正文
加密算法的历史
加密算法最早诞生在什么时候?早在古罗马时期,加密算法就被应用于战争当中。
在大规模的战争中,部队之间常常需要信使往来,传递重要的军事情报。 可是,一旦信使被敌军抓获,重要的军事情报就完全暴露给了敌方。 甚至,狡猾的敌人有可能篡改军事情报,并收买信使把假情报传递给我方部队。 这样一来,我方部队就完全落入到了敌方的陷阱之中。这种拦截并篡改信息的手法,在网络安全领域被称为中间人攻击。
怎样防止这种情况的发生呢?不让信使被敌人抓获?这个肯定是无法绝对避免的。 那么我们不妨换个角度,让敌人即使截获了军事情报,也看不懂里面的内容,这就是对信息的加密。
如何进行加密呢?古人想出了一种非常朴素的加密方法,被称为凯撒密码。加密的原理就像下图这样:
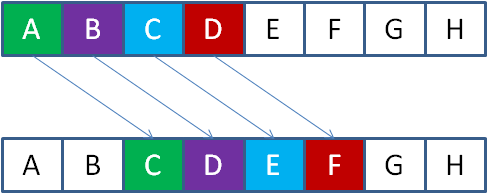
如图所示,图中第一行的字母代表信息的“明文”,第二行字母代表信息的密文。这个加密算法十分简单,就是选择一个偏移量(这里的偏移量是2), 把明文当中的所有字母按照字母表的顺序向后偏移两位,从而生成密文。比如:
原文的字母A,对应的密文是字母C。
原文的字母D,对应的密文是字母F。
原文的单词Java,对应的密文是Lcxc。
这样一来,敌方看到信使的情报内容,就彻底蒙逼了。相应的,我军事先约定好了密文通信的偏移量,当友军收到情报以后, 把密文的所有字母向前偏移两位,就还原成了明文,这个过程叫做解密。
但是,这种加密方法真的百分百保险吗?并不是。
在英语的26个字母中,出现频率最高的字母是e。如果敌人截获了情报,发现这段看不懂的密文当中出现频率最高的字母是g, 由于e和g相差两个字母,就可以猜测出我军的密文通信很可能选择2作为偏移量。这样一来,我军的密码就被破解了。
最不济,敌人可以把每一种偏移量都尝试一遍(26个字母,最多25种偏移),终究可以试出符合正常语法的偏移量。这种方式被称为暴力破解。
加密算法的种类
在如今的信息安全领域,有各种各样的加密算法凝聚了计算机科学家们的智慧。 从宏观上来看,这些加密算法可以归结为三大类:哈希算法、对称加密算法、非对称加密算法。
哈希算法
从严格意义上来说,哈希算法并不属于加密算法,但它在信息安全领域起到了很重要的作用。
哈希算法能做什么用呢?其中一个重要的作用就是生成信息摘要,用以验证原信息的完整性和来源的可靠性。
让我们来举个栗子:
在某个互联网应用上,有用户下单买了东西,于是应用需要通知支付宝,并告诉支付宝商户ID、支付金额等等信息。
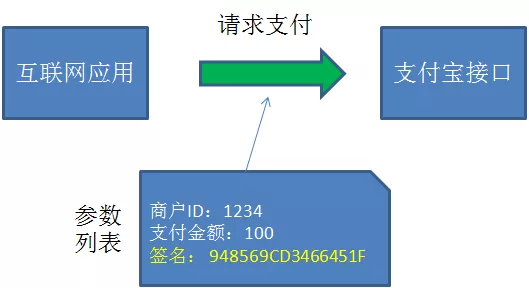
支付宝怎么知道这个请求是真的来自该应用,并且没有被篡改呢?
请求的发送方把所有参数,外加双方约定的Key(例子中Key=abc)拼接起来,并利用哈希算法生成了一段信息摘要:
Hash(1234_100_abc) = 948569CD3466451F
而请求的接收方在接到参数和摘要之后,按照同样的规则,也把参数和Key拼接起来并生成摘要:
Hash(1234_100_abc) = 948569CD3466451F
如果最终发现两端信息摘要一致,证明信息没有被篡改,并且来源确实是该互联网应用。 (只要参数修改了一点点,或者Key不一样,那么生成的信息摘要就会完全不同)
生成信息摘要的过程叫做签名,验证信息摘要的过程叫做验签。
哈希算法包含哪些具体的算法呢?其中最著名的当属MD5算法。 后来,人们觉得MD5算法生成的信息摘要太短(128位),不够安全,于是又有了SHA系列算法。
对称加密算法
哈希算法可以解决验签的问题,却无法解决明文加密的问题。这时候,就需要真正的加密算法出场了。
什么是对称加密呢?这个概念很好理解:
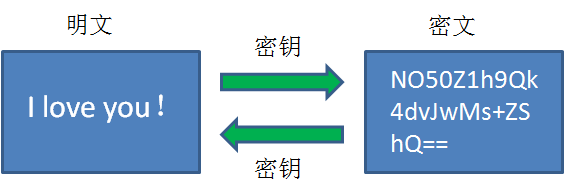
如图所示,一段明文通过密钥进行加密,可以生成一段密文;这段密文通过同样的密钥进行解密,可以还原成明文。 这样一来,只要双方事先约定好了密钥,就可以使用密文进行往来通信。
除了通信过程中的加密以外,数据库存储的敏感信息也可以通过这种方式进行加密。这样即使数据泄露到了外界,泄露出去的也都是密文。
对称加密包含哪些具体的算法呢?在早期,人们使用DES算法(Data Encryption Standard)进行加密解密;后来,人们觉得DES不够安全,发明了3DES算法; 而如今,最为流行的对称加密算法是AES算法(Advanced Encryption Standard)。
不知道读者中有多少人曾经接触过欧盟的GDPR法案,为了遵从该法案,有的企业就曾经将数据库中的敏感信息使用3DES进行加密。
总而言之,对称算法的好处是加密解密的效率比较高。相应的,对称算法的缺点是不够安全。 为什么呢?通信双方约定的密钥是相同的,只要密钥本身被任何一方泄露出去,通信的密文就会被破解; 此外,在双方建立通信之初,服务端把密钥告诉给客户端的时候,也有被拦截到的危险。
为了解决这一痛点,非对称加密就登场了。
非对称加密算法
什么又是非对称加密呢?在刚刚接触到的时候,或许你会觉得这种算法有些古怪:
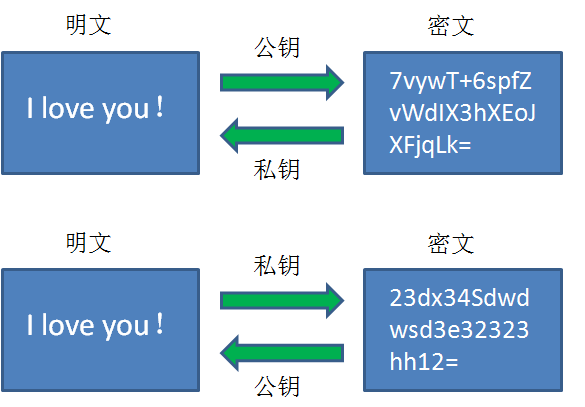
如图所示,在非对称加密中存在一对密钥,其中一个叫做公钥,另一个叫做私钥。 在加密解密的过程中,我们既可以使用公钥加密明文,使用私钥解密密文;也可以使用私钥加密明文,使用公钥解密密文。
这样设计有什么好处呢?看看通信的过程就知道了:
- 在双方建立通信的时候,服务端只要把公钥告诉给客户端,自己保留私钥。
- 客户端利用获得的公钥。加密另外一个密钥X(可以是对称加密的密钥),发送给服务端。
- 服务端获得消息后,用自己的私钥解密,得到里面隐含的密钥X。
- 从此以后,双方可以利用密钥X进行对称加密的通信了。
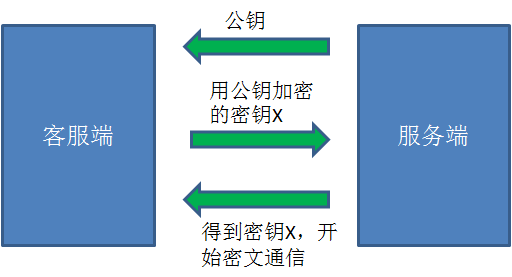
在这个过程中,即使公钥被第三方截获,甚至后续的所有通信都被截获,第三方也无法进行破解。 因为第二步利用公钥加密的消息,只有私钥才能解开,所以第三方永远无法知道密钥X是什么。
非对称加密算法的代表有哪些呢?最著名的当属RSA算法。
既然非对称加密这么强大,是不是没有缺点呢?也不是。非对称加密最大的问题,就是性能较差,无法应用于长期的通信。
具体算法
MD5算法
MD5信息摘要算法(Message-Digest Algorithm 5),一种被广泛使用的密码散列函数, 可以产生出一个128位(16字节)的散列值(hash value),用于确保信息传输完整一致。
摘要哈希生成的正确姿势是什么样呢?分三步:
- 收集相关业务参数,在这里是金额和目标账户。当然,实际应用中的参数肯定比这多得多,这里只是做了简化。
- 按照规则,把参数名和参数值拼接成一个字符串,同时把给定的密钥也拼接起来。之所以需要密钥,是因为攻击者也可能获知拼接规则。
- 利用MD5算法,从原文生成哈希值。MD5生成的哈希值是128位的二进制数,也就是32位的十六进制数。
Hash(1234_100_abc) = 948569CD3466451F
第三方支付平台如何验证请求的签名?同样分三步:
- 发送方和请求方约定相同的字符串拼接规则,约定相同的密钥。
- 第三方平台接到支付请求,按规则拼接业务参数和密钥,利用MD5算法生成Sign。
- 用第三方平台自己生成的Sign和请求发送过来的Sign做对比,如果两个Sign值一模一样,则签名无误,如果两个Sign值不同,则信息做了篡改。这个过程叫做验签。
Hash(1234_100_abc) = 948569CD3466451F
MD5算法底层原理:
简单概括起来,MD5算法的过程分为四步:处理原文,设置初始值,循环加工,拼接结果。
第一步:处理原文
首先,我们计算出原文长度(bit)对512求余的结果,如果不等于448,就需要填充原文使得原文对512求余的结果等于448。
填充的方法是第一位填充1,其余位填充0。填充完后,信息的长度就是512*N+448。
之后,用剩余的位置(512-448=64位)记录原文的真正长度,把长度的二进制值补在最后。这样处理后的信息长度就是512*(N+1)。
第二步:设置初始值
MD5的哈希结果长度为128位,按每32位分成一组共4组。这4组结果是由4个初始值A、B、C、D经过不断演变得到。 MD5的官方实现中,A、B、C、D的初始值如下(16进制):
A=0x01234567
B=0x89ABCDEF
C=0xFEDCBA98
D=0x76543210
第三步:循环加工
这一步是最复杂的一步,我们看看下面这张图,此图代表了单次A,B,C,D值演变的流程。
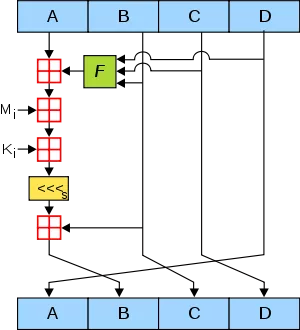
图中,A,B,C,D就是哈希值的四个分组。每一次循环都会让旧的ABCD产生新的ABCD。一共进行多少次循环呢?由处理后的原文长度决定。
假设处理后的原文长度是M
主循环次数 = M / 512
每个主循环中包含 512 / 32 * 4 = 64 次 子循环。
上面这张图所表达的就是单次子循环的流程。
下面对图中其他元素一一解释:
1.绿色F
图中的绿色F,代表非线性函数。官方MD5所用到的函数有四种:
F(X, Y, Z) =(X&Y) | ((~X) & Z)
G(X, Y, Z) =(X&Z) | (Y & (~Z))
H(X, Y, Z) =X^Y^Z
I(X, Y, Z)=Y^(X|(~Z))
在主循环下面64次子循环中,F、G、H、I 交替使用,第一个16次使用F,第二个16次使用G,第三个16次使用H,第四个16次使用I。
2.红色“田”字
很简单,红色的田字代表相加的意思。
3.Mi
Mi是第一步处理后的原文。在第一步中,处理后原文的长度是512的整数倍。把原文的每512位再分成16等份,命名为M0~M15,每一等份长度32。 在64次子循环中,每16次循环,都会交替用到M1~M16之一。
4.Ki
一个常量,在64次子循环中,每一次用到的常量都是不同的。
5.黄色的«<S
左移S位,S的值也是常量。
“流水线”的最后,让计算的结果和B相加,取代原先的B。新ABCD的产生可以归纳为:
新A = 原d
新B = b+((a+F(b,c,d)+Mj+Ki)<<<s)
新C = 原b
新D = 原c
总结一下主循环中的64次子循环,可以归纳为下面的四部分:
第一轮:
FF(a,b,c,d,M0,7,0xd76aa478) s[0]=7, K[0] = 0xd76aa478
FF(a,b,c,d,M1,12,0xe8c7b756) s[1]=12, K[1] = 0xe8c7b756
FF(a,b,c,d,M2,17,0x242070db)
FF(a,b,c,d,M3,22,0xc1bdceee)
FF(a,b,c,d,M4,7,0xf57c0faf)
FF(a,b,c,d,M5,12,0x4787c62a)
FF(a,b,c,d,M6,17,0xa8304613)
FF(a,b,c,d,M7,22,0xfd469501)
FF(a,b,c,d,M8,7,0x698098d8)
FF(a,b,c,d,M9,12,0x8b44f7af)
FF(a,b,c,d,M10,17,0xffff5bb1)
FF(a,b,c,d,M11,22,0x895cd7be)
FF(a,b,c,d,M12,7,0x6b901122)
FF(a,b,c,d,M13,12,0xfd987193)
FF(a,b,c,d,M14,17, 0xa679438e)
FF(a,b,c,d,M15,22,0x49b40821)
第二轮:
GG(a,b,c,d,M1,5,0xf61e2562)
GG(a,b,c,d,M6,9,0xc040b340)
GG(a,b,c,d,M11,14,0x265e5a51)
GG(a,b,c,d,M0,20,0xe9b6c7aa)
GG(a,b,c,d,M5,5,0xd62f105d)
GG(a,b,c,d,M10,9,0x02441453)
GG(a,b,c,d,M15,14,0xd8a1e681)
GG(a,b,c,d,M4,20,0xe7d3fbc8)
GG(a,b,c,d,M9,5,0x21e1cde6)
GG(a,b,c,d,M14,9,0xc33707d6)
GG(a,b,c,d,M3,14,0xf4d50d87)
GG(a,b,c,d,M8,20,0x455a14ed)
GG(a,b,c,d,M13,5,0xa9e3e905)
GG(a,b,c,d,M2,9,0xfcefa3f8)
GG(a,b,c,d,M7,14,0x676f02d9)
GG(a,b,c,d,M12,20,0x8d2a4c8a)
第三轮:
HH(a,b,c,d,M5,4,0xfffa3942)
HH(a,b,c,d,M8,11,0x8771f681)
HH(a,b,c,d,M11,16,0x6d9d6122)
HH(a,b,c,d,M14,23,0xfde5380c)
HH(a,b,c,d,M1,4,0xa4beea44)
HH(a,b,c,d,M4,11,0x4bdecfa9)
HH(a,b,c,d,M7,16,0xf6bb4b60)
HH(a,b,c,d,M10,23,0xbebfbc70)
HH(a,b,c,d,M13,4,0x289b7ec6)
HH(a,b,c,d,M0,11,0xeaa127fa)
HH(a,b,c,d,M3,16,0xd4ef3085)
HH(a,b,c,d,M6,23,0x04881d05)
HH(a,b,c,d,M9,4,0xd9d4d039)
HH(a,b,c,d,M12,11,0xe6db99e5)
HH(a,b,c,d,M15,16,0x1fa27cf8)
HH(a,b,c,d,M2,23,0xc4ac5665)
第四轮:
Ⅱ(a,b,c,d,M0,6,0xf4292244)
Ⅱ(a,b,c,d,M7,10,0x432aff97)
Ⅱ(a,b,c,d,M14,15,0xab9423a7)
Ⅱ(a,b,c,d,M5,21,0xfc93a039)
Ⅱ(a,b,c,d,M12,6,0x655b59c3)
Ⅱ(a,b,c,d,M3,10,0x8f0ccc92)
Ⅱ(a,b,c,d,M10,15,0xffeff47d)
Ⅱ(a,b,c,d,M1,21,0x85845dd1)
Ⅱ(a,b,c,d,M8,6,0x6fa87e4f)
Ⅱ(a,b,c,d,M15,10,0xfe2ce6e0)
Ⅱ(a,b,c,d,M6,15,0xa3014314)
Ⅱ(a,b,c,d,M13,21,0x4e0811a1)
Ⅱ(a,b,c,d,M4,6,0xf7537e82)
Ⅱ(a,b,c,d,M11,10,0xbd3af235)
Ⅱ(a,b,c,d,M2,15,0x2ad7d2bb)
Ⅱ(a,b,c,d,M9,21,0xeb86d391)
第四步:拼接结果
这一步就很简单了,把循环加工最终产生的A,B,C,D四个值拼接在一起,转换成字符串即可。
破解MD5算法
这里说的破解,并非把摘要还原成原文,而是通过碰撞生成相同的密文摘要。
设MD5的哈希函数是H(X),那么:
H(A) = M
H(B) = M
任意一个B即为破解结果。
B有可能等于A,也可能不等于A。
用一个形象的说法,A和B的MD5结果“殊途同归”。
碰撞方法有:
暴力枚举法 ,时间换空间
字典法 ,空间换时间
彩虹表法
2004年,王小云教授提出了非常高效的MD5碰撞方法。
2009年,冯登国、谢涛利用差分攻击,将MD5的碰撞算法复杂度进一步降低。
SHA系列算法
SHA (Secure Hash Algorithm) 安全散列算法,也是生成信息摘要的算法。
SHA-1
SHA-1算法可以从明文生成160bit的信息摘要,示例如下:
给定明文: abcd
SHA-1摘要: 81FE8BFE87576C3ECB22426F8E57847382917ACF
SHA-1 与 MD5的主要区别是什么呢?
1.摘要长度不同。
MD5的摘要的长度为128bit,SHA-1的摘要长度是160bit。多出32bit意味着什么呢?不同明文的碰撞几率降低了2^32 = 324294967296倍。
2.性能略有差别
SHA-1生成摘要的性能比MD5略低。
2005年,SHA-1被破解了。
SHA-2
SHA-2是一系列SHA算法变体的总称,其中包含如下子版本:
SHA-256:可以生成长度256bit的信息摘要。
SHA-224:SHA-256的“阉割版”,可以生成长度224bit的信息摘要。
SHA-512:可以生成长度512bit的信息摘要。
SHA-384:SHA-512的“阉割版”,可以生成长度384bit的信息摘要。
显然,信息摘要越长,发生碰撞的几率就越低,破解的难度就越大。但同时,耗费的性能和占用的空间也就越高。
为了安全,可以多种摘要算法结合使用:
明文: abcd
MD5摘要: e2fc714c4727ee9395f324cd2e7f331f
SHA-256摘要: 88d4266fd4e6338d13b845fcf289579d209c897823b9217da3e161936f031589
合成摘要: e2fc714c4727ee93209c897823b9217da3e161936f031589
取MD5摘要的前16位 和 SHA-256摘要的后32位,拼成一个长度为48位的合成摘要。
SHA算法的底层原理和MD5很相似,只是在摘要分段和处理细节上有少许差别。
简而言之,MD5把128bit的信息摘要分成A,B,C,D四段(Words),每段32bit,在循环过程中交替运算A,B,C,D,最终组成128bit的摘要结果。

再看一下SHA-1算法,核心过程大同小异,主要的不同点是把160bit的信息摘要分成了A,B,C,D,E五段。
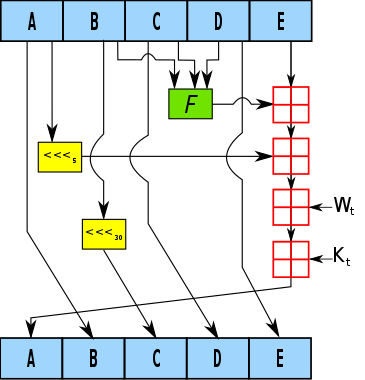
其中SHA-256的每一段摘要长度是32bit,SHA-512的每一段摘要长度是64bit。SHA-224和SHA-384则是在前两者生成结果的基础上做出裁剪。
SHA家族的最新成员SHA-3已经于2015年问世。
AES算法
AES,高级加密标准(英语:Advanced Encryption Standard,缩写:AES),在密码学中又称Rijndael加密法,是美国联邦政府采用的一种区块加密标准。 这个标准用来替代原先的DES,已经被多方分析且广为全世界所使用。

具体工作的步骤如下:
- 发送方利用密钥
123456,加密明文“我是小灰”,加密结果为TNYRvx+SNjZwEK+ZXFEcDw==。 - 发送方把加密后的内容
TNYRvx+SNjZwEK+ZXFEcDw==传输给接收方。 - 接收方收到密文
TNYRvx+SNjZwEK+ZXFEcDw==,利用密钥123456还原为明文“我是小灰”。
1.密钥
密钥是AES算法实现加密和解密的根本。对称加密算法之所以对称,是因为这类算法对明文的加密和解密需要使用同一个密钥。
AES支持三种长度的密钥: 128位,192位,256位
平时大家所说的AES128,AES192,AES256,实际上就是指的AES算法对不同长度密钥的使用。
2.填充
要想了解填充的概念,我们先要了解AES的分组加密特性。
什么是分组加密呢?我们来看看下面这张图:
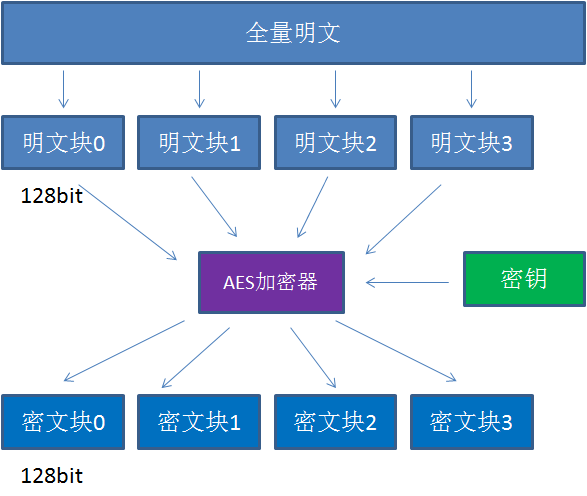
AES算法在对明文加密的时候,并不是把整个明文一股脑加密成一整段密文,而是把明文拆分成一个个独立的明文块,每一个明文块长度128bit。
这些明文块经过AES加密器的复杂处理,生成一个个独立的密文块,这些密文块拼接在一起,就是最终的AES加密结果。
但是这里涉及到一个问题:
假如一段明文长度是192bit,如果按每128bit一个明文块来拆分的话,第二个明文块只有64bit,不足128bit。 这时候怎么办呢?就需要对明文块进行填充(Padding)。
NoPadding:
不做任何填充,但是要求明文必须是16字节的整数倍。
PKCS5Padding(默认):
如果明文块少于16个字节(128bit),在明文块末尾补足相应数量的字符,且每个字节的值等于缺少的字符数。
比如明文:{1,2,3,4,5,a,b,c,d,e},缺少6个字节,则补全为{1,2,3,4,5,a,b,c,d,e,6,6,6,6,6,6}
ISO10126Padding:
如果明文块少于16个字节(128bit),在明文块末尾补足相应数量的字节,最后一个字符值等于缺少的字符数,其他字符填充随机数。
比如明文:{1,2,3,4,5,a,b,c,d,e},缺少6个字节,则可能补全为{1,2,3,4,5,a,b,c,d,e,5,c,3,G,$,6}
3.模式
AES的工作模式,体现在把明文块加密成密文块的处理过程中。AES加密算法提供了五种不同的工作模式:
ECB、CBC、CTR、CFB、OFB
模式之间的主题思想是近似的,在处理细节上有一些差别。
ECB模式(默认):
电码本模式 Electronic Codebook Book
CBC模式:
密码分组链接模式 Cipher Block Chaining
CTR模式:
计算器模式 Counter
CFB模式:
密码反馈模式 Cipher FeedBack
OFB模式:
输出反馈模式 Output FeedBack
几点补充:
- 我们在调用封装好的AES算法时,表面上使用的Key并不是真正用于AES加密解密的密钥,而是用于生成真正密钥的“种子”。
- 填充明文时,如果明文长度原本就是16字节的整数倍,那么除了NoPadding以外,其他的填充方式都会填充一组额外的16字节明文块。
以上就是AES的基本概念。
下面来给大家讲一讲AES算法的底层原理。
在这里我们重新梳理一下:
- 把明文按照128bit拆分成若干个明文块。
- 按照选择的填充方式来填充最后一个明文块。
- 每一个明文块利用AES加密器和密钥,加密成密文块。
- 拼接所有的密文块,成为最终的密文结果。
AES加密器:
具体分成多少轮呢?
初始轮(Initial Round) 1次
普通轮(Rounds) N次
最终轮(Final Round) 1次
上一期我们提到,AES的Key支持三种长度:AES128,AES192,AES256。Key的长度决定了AES加密的轮数。
除去初始轮,各种Key长度对应的轮数如下:
AES128:10轮
AES192:12轮
AES256:14轮
不同阶段的Round有不同的处理步骤。
初始轮只有一个步骤:
加轮密钥(AddRoundKey)
普通轮有四个步骤:
字节代替(SubBytes)
行移位(ShiftRows)
列混淆(MixColumns)
加轮密钥(AddRoundKey)
最终轮有三个步骤:
字节代替(SubBytes)
行移位(ShiftRows)
加轮密钥(AddRoundKey)
步骤解说:
1.字节替代(SubBytes)
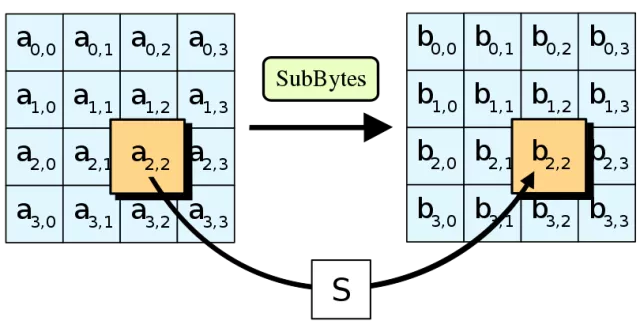
首先需要说明的是,16字节的明文块在每一个处理步骤中都被排列成4X4的二维数组。
所谓字节替代,就是把明文块的每一个字节都替代成另外一个字节。替代的依据是什么呢?依据一个被称为S盒(Subtitution Box)的16X16大小的二维常量数组。
假设明文块当中a[2,2] = 5B(一个字节是两位16进制),那么输出值b[2,2] = S[5][11]。
2.行移位(ShiftRows)
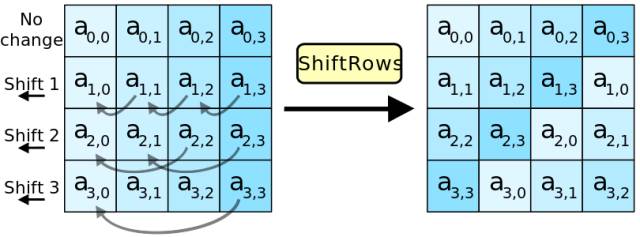
这一步很简单,就像图中所描述的:
第一行不变
第二行循环左移1个字节
第三行循环左移2个字节
第四行循环左移3个字节
3.列混淆(MixColumns)
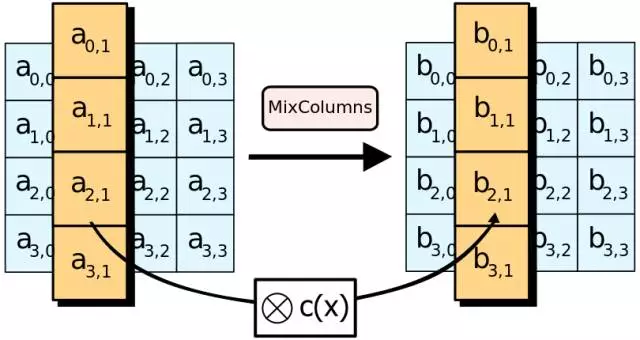
这一步,输入数组的每一列要和一个名为修补矩阵(fixed matrix)的二维常量数组做矩阵相乘,得到对应的输出列。
4.加轮密钥(AddRoundKey)
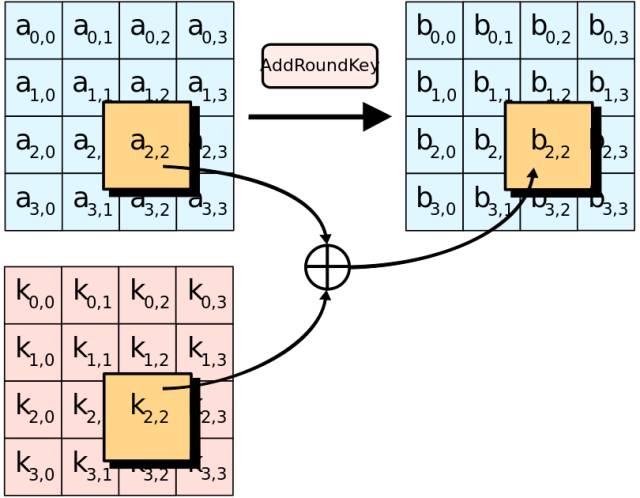
这一步是唯一利用到密钥的一步,128bit的密钥也同样被排列成4X4的矩阵。
让输入数组的每一个字节a[i,j]与密钥对应位置的字节k[i,j]异或一次,就生成了输出值b[i,j]。
需要补充一点,加密的每一轮所用到的密钥并不是相同的。这里涉及到一个概念:扩展密钥(KeyExpansions)。
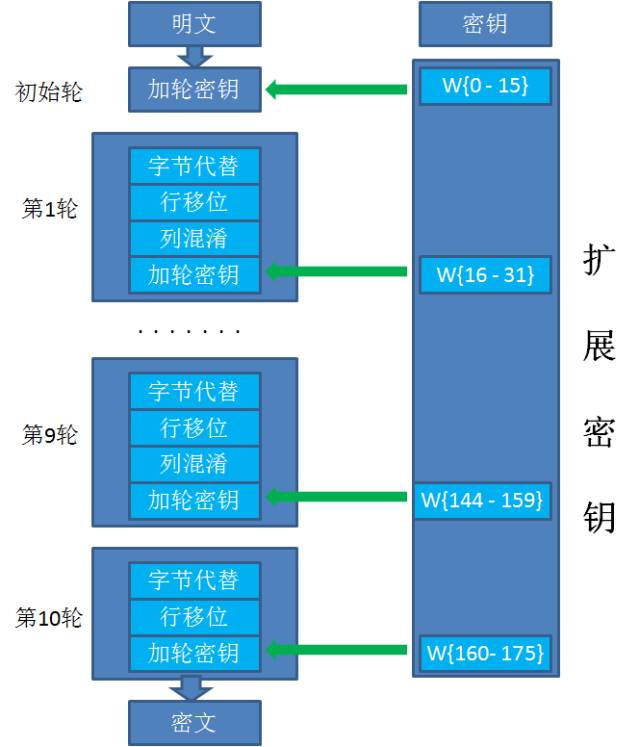
扩展密钥(KeyExpansions)
AES源代码中用长度 4 * 4 *(10+1) 字节的数组W来存储所有轮的密钥。W{0-15}的值等同于原始密钥的值,用于为初始轮做处理。
后续每一个元素W[i]都是由W[i-4]和W[i-1]计算而来,直到数组W的所有元素都赋值完成。
W数组当中,W{0-15}用于初始轮的处理,W{16-31}用于第1轮的处理,W{32-47}用于第2轮的处理 ……一直到W{160-175}用于最终轮(第10轮)的处理。
解密流程就是把加密流程倒置过来:最终轮,普通轮,初始轮。扩展密钥的使用顺序也和加密相反。
下面拓展说一下工作模式:
1.ECB模式
ECB模式(Electronic Codebook Book)是最简单的工作模式,在该模式下,每一个明文块的加密都是完全独立,互不干涉的。
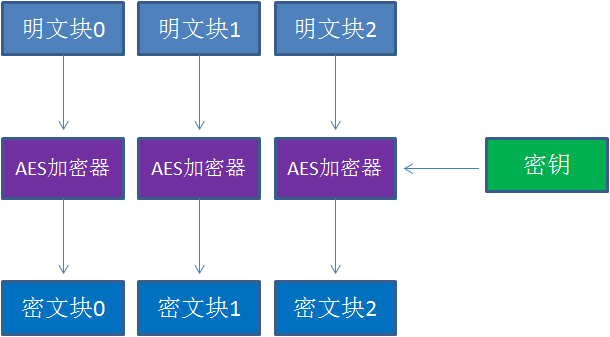
这样的好处是什么呢?
- 简单
- 有利于并行计算
缺点同样也很明显:
相同的明文块经过加密会变成相同的密文块,因此安全性较差。
2.CBC模式
CBC模式(Cipher Block Chaining)引入了一个新的概念:初始向量IV(Initialization Vector)。
IV是做什么用的呢?它的作用和MD5的“加盐”有些类似,目的是防止同样的明文块始终加密成同样的密文块。
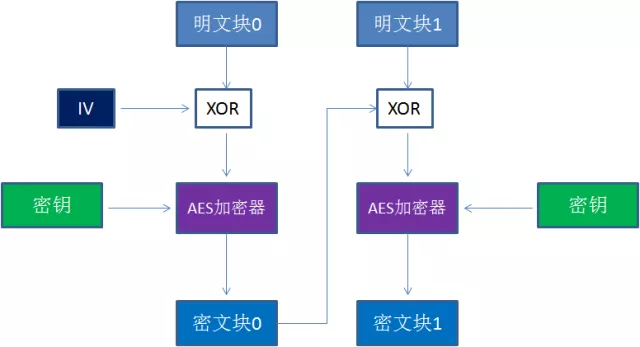
从图中可以看出,CBC模式在每一个明文块加密前会让明文块和一个值先做异或操作。 IV作为初始化变量,参与第一个明文块的异或,后续的每一个明文块和它前一个明文块所加密出的密文块相异或。
这样以来,相同的明文块加密出的密文块显然是不一样的。
CBC模式的好处是什么呢?
安全性更高
坏处也很明显:
- 无法并行计算,性能上不如ECB
- 引入初始化向量IV,增加复杂度。
RSA算法
RSA公钥加密算法是1977年由Ron Rivest、Adi Shamirh和LenAdleman在(美国麻省理工学院)开发的。 RSA取名来自开发他们三者的名字。RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的所有密码攻击, 已被ISO推荐为公钥数据加密标准。RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易, 但那时想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
在线生成公私匙 http://www.metools.info/code/c80.html
代码实现
PHP版RSA
<?php
/**
* RSA签名类
*/
class Rsa
{
public $publicKey = '';
public $privateKey = '';
private $_privKey;
/**
* * private key
*/
private $_pubKey;
/**
* * public key
*/
private $_keyPath;
/**
* * the keys saving path
*/
/**
* * the construtor,the param $path is the keys saving path
* @param string $publicKey 公钥
* @param string $privateKey 私钥
*/
public function __construct($publicKey = null, $privateKey = null)
{
$this->setKey($publicKey, $privateKey);
}
/**
* 设置公钥和私钥
* @param string $publicKey 公钥
* @param string $privateKey 私钥
*/
public function setKey($publicKey = null, $privateKey = null)
{
if (!is_null($publicKey)) {
$this->publicKey = $publicKey;
}
if (!is_null($privateKey)) {
$this->privateKey = $privateKey;
}
}
/**
* * setup the private key
*/
private function setupPrivKey()
{
if (is_resource($this->_privKey)) {
return true;
}
$pem = chunk_split($this->privateKey, 64, "\n");
$pem = "-----BEGIN PRIVATE KEY-----\n" . $pem . "-----END PRIVATE KEY-----\n";
$this->_privKey = openssl_pkey_get_private($pem);
return true;
}
/**
* * setup the public key
*/
private function setupPubKey()
{
if (is_resource($this->_pubKey)) {
return true;
}
$pem = chunk_split($this->publicKey, 64, "\n");
$pem = "-----BEGIN PUBLIC KEY-----\n" . $pem . "-----END PUBLIC KEY-----\n";
$this->_pubKey = openssl_pkey_get_public($pem);
return true;
}
/**
* * encrypt with the private key
*/
public function privEncrypt($data)
{
if (!is_string($data)) {
return null;
}
$this->setupPrivKey();
$r = openssl_private_encrypt($data, $encrypted, $this->_privKey);
if ($r) {
return base64_encode($encrypted);
}
return null;
}
/**
* * decrypt with the private key
*/
public function privDecrypt($encrypted)
{
if (!is_string($encrypted)) {
return null;
}
$this->setupPrivKey();
$encrypted = base64_decode($encrypted);
$r = openssl_private_decrypt($encrypted, $decrypted, $this->_privKey);
if ($r) {
return $decrypted;
}
return null;
}
/**
* * encrypt with public key
*/
public function pubEncrypt($data)
{
if (!is_string($data)) {
return null;
}
$this->setupPubKey();
$r = openssl_public_encrypt($data, $encrypted, $this->_pubKey);
if ($r) {
return base64_encode($encrypted);
}
return null;
}
/**
* * decrypt with the public key
*/
public function pubDecrypt($crypted)
{
if (!is_string($crypted)) {
return null;
}
$this->setupPubKey();
$crypted = base64_decode($crypted);
$r = openssl_public_decrypt($crypted, $decrypted, $this->_pubKey);
if ($r) {
return $decrypted;
}
return null;
}
/**
* 构造签名
* @param string $dataString 被签名数据
* @return string
*/
public function sign($dataString)
{
$this->setupPrivKey();
$signature = false;
openssl_sign($dataString, $signature, $this->_privKey);
return base64_encode($signature);
}
/**
* 验证签名
* @param string $dataString 被签名数据
* @param string $signString 已经签名的字符串
* @return number 1签名正确 0签名错误
*/
public function verify($dataString, $signString)
{
$this->setupPubKey();
$signature = base64_decode($signString);
$flg = openssl_verify($dataString, $signature, $this->_pubKey);
return $flg;
}
public function __destruct()
{
is_resource($this->_privKey) && @openssl_free_key($this->_privKey);
is_resource($this->_pubKey) && @openssl_free_key($this->_pubKey);
}
}
$publicKey = 'MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAKZ1mKTymRoGKnHiP1xAy4aiyt5r0BscCZnDAonCrMFZ4kBGriPNHxEaLr5lfBnMKw7k6i+2dsFPSEZooTvqtPUCAwEAAQ==';
$privateKey = 'MIIBVAIBADANBgkqhkiG9w0BAQEFAASCAT4wggE6AgEAAkEApnWYpPKZGgYqceI/XEDLhqLK3mvQGxwJmcMCicKswVniQEauI80fERouvmV8GcwrDuTqL7Z2wU9IRmihO+q09QIDAQABAkBunx3nGHXYjppsfn++7iyTd+I7+Agfy/0xWyB3rpEiGGgfemjcRFaeq5SC2vUNXsrEOY5gbUSQmFxH//Cym18NAiEA1z1cZx/Q9cbIjFPwp1a+K5CVFDXDcfbi/AQgAkVs0/cCIQDF+2fr23AoBslcOC4S0yAx94AbgxCntYuRqztxybsrcwIgMW86ZcT87TX2oaQ1xXk6vC68zqN6fBZEE7Wu1Fa1pAkCIElmOJP3qfAc/AAlj+dIwLHlqWgJwl3674CU9Bfui2bDAiEA0CKJpF8x7KANCcopEQC93PsbIztuML322LOfDV1Lw/k=';
$rsa = new Rsa($publicKey, $privateKey);
$str = "abc";
echo "原始数据:" . $str;
echo "<br/><hr>";
$res = $rsa->privEncrypt($str);
echo "私钥加密数据:" . $res;
echo "<br/>";
$res2 = $rsa->pubDecrypt($res);
echo "公钥解密数据:" . $res2;
echo "<br/><hr>";
$res3 = $rsa->pubEncrypt($str);
echo "公钥加密数据:" . $res3;
echo "<br/>";
$res4 = $rsa->privDecrypt($res3);
echo "私钥解密数据:" . $res4;
echo "<br/><hr>";
echo "签名数据:" . $str;
$res5 = $rsa->sign($str);
echo "<br/>";
echo "签名结果:" . $res5;
$res6 = $rsa->verify($str, $res5);
echo "<br/>";
echo "验证签结果:" . $res6;
输出:
原始数据:abc
私钥加密数据:Ty08uQ+/TZ0A2o1n7Vz4H+qfhBGMf/0k6AeoablnoAuLqku20btTQ0/Q0SVkAlc0pT7BhEX2CNr5ywOPYDX7Nw==
公钥解密数据:abc
公钥加密数据:BT+e96vz/xzMS5rNPt78ozYJ3dTeJ6lCwUVzkhknBT00OtLWJy6XXmSKwOhG7xhN8rXrQ51o5hOeHC8ngj7wYQ==
私钥解密数据:abc
签名数据:abc
签名结果:jatP2AsWxNo64VuSp1vrzYI2qfDmvV829b6CgRh65tddy5HrTHB5zQcjf66tA2lUTNFHVHucqwr0qiwxYFcdtA==
验证签结果:1