图解计算机
我和小宇早恋了,我们家住隔壁。
一、编码与电路——信号的转换
晚上父母会把手机没收,但我们还想继续聊天,又不敢发出声音,于是我们想到了这个办法…
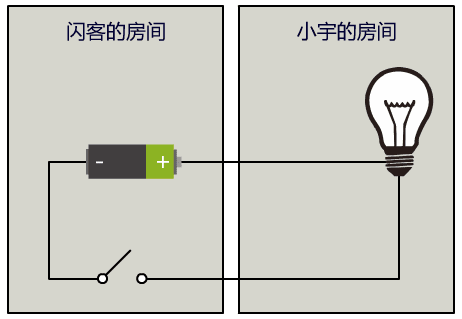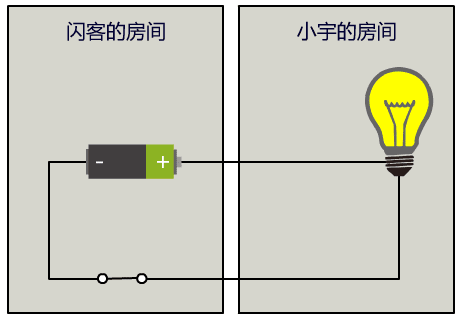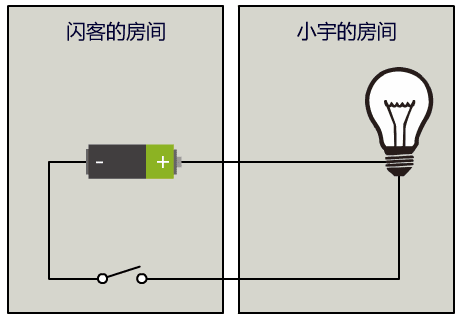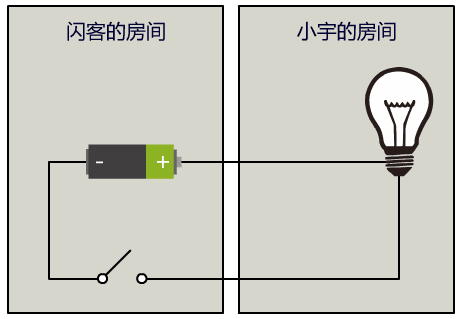
我们把所有的中文都用灯泡的亮灭组合来表示,同时约定好每隔一秒读取一次灯泡的状态并记录下来,这是我们的暗号。
我:亮亮灭灭亮
喜:灭亮亮灭灭
欢:亮灭亮灭亮
你:亮亮亮灭灭
这样,我们虽然没有了手机,依然可以日以继日地聊天,虽然效率很低,但依然很快乐。
我和小宇就这样在不经意间,将语言转换成为了灯泡的亮灭组合,这个过程叫做编码。
二、门电路——信号的关联
我和小宇就这样一直秘密保持着通话,直到上了大学,父母再也管不了我们用手机了。
但这么多年的小灯泡通话,使我们总觉得事情没那么简单,于是我们开始了一些新的探索。
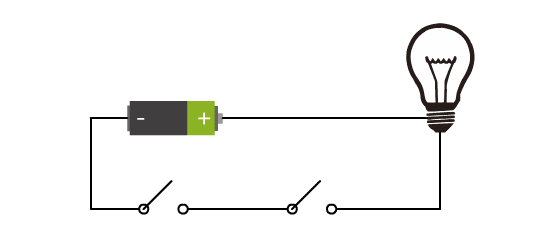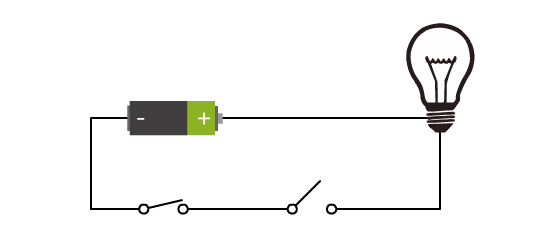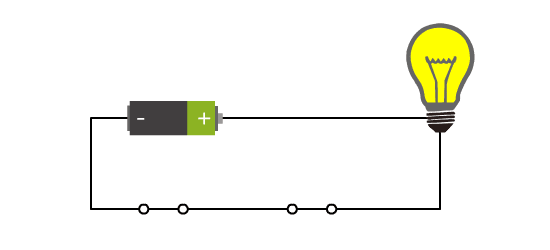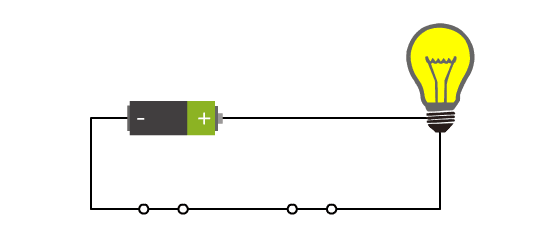
我们增加了一个开关。此时当两个开关同时闭合时,灯泡才会亮。
这样两个开关与灯泡之间,不再是之前简单的对应关系了,而是有了逻辑。
开关的断开与闭合分别对应着电路的断开与连通。而小灯泡的不亮与亮,也分别对应着电路的断开与连通。 那这两者就可以统一,不再依赖于具体的实物表现了。
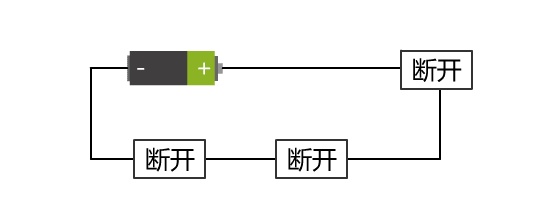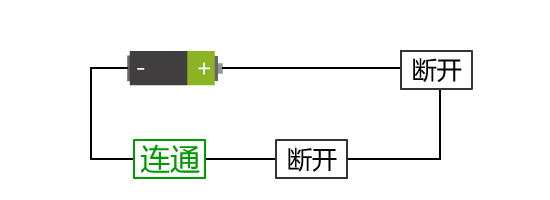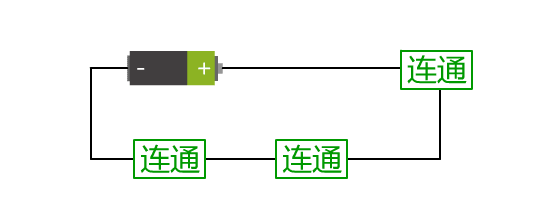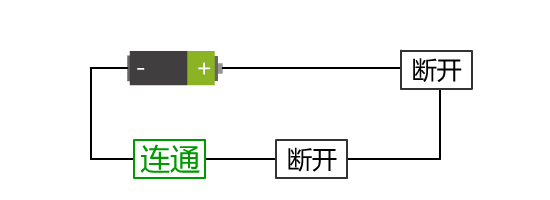
还有,开关的连通与断开,是主动的。而小灯泡的连通与断开,是被动的,是结果。
我们把开关这里的连通与断开称为输入端,把灯泡的连通与断开称为输出端,并且将整个电路都封装在一个图形里,可以得到如下抽象:
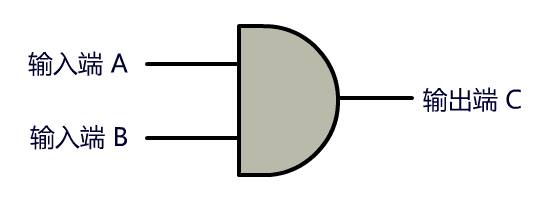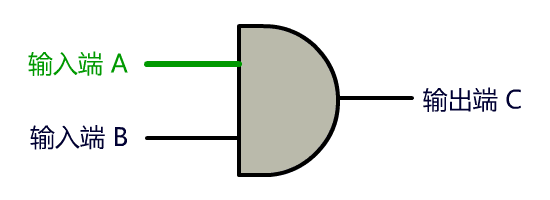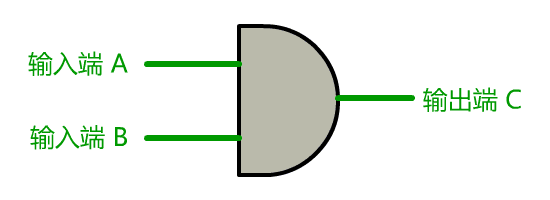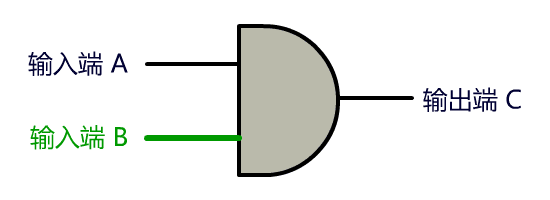
我们决定把这种电路叫做门电路, 上面这个叫与门。
为了今后更为抽象的探索,我们将电路连通表示为数字 1,电路断开表示为数字 0。
我们将这种表示方式称为二进制。
输入 A 输入 B 输出
0 0 0
0 1 0
1 0 0
1 1 1
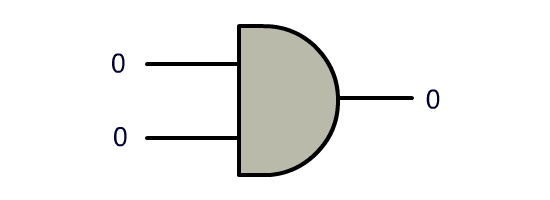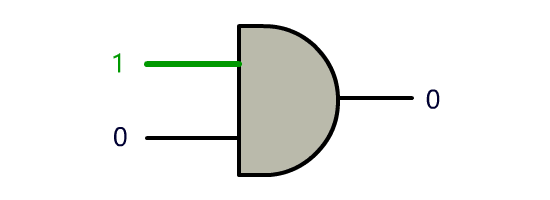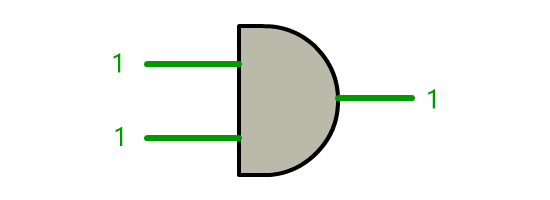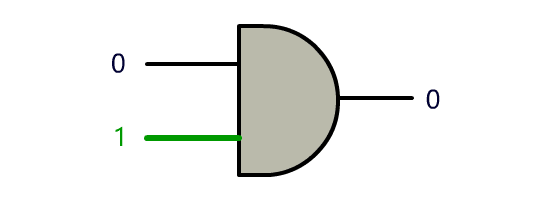
慢慢地,我们发现了越来越多的玩法。
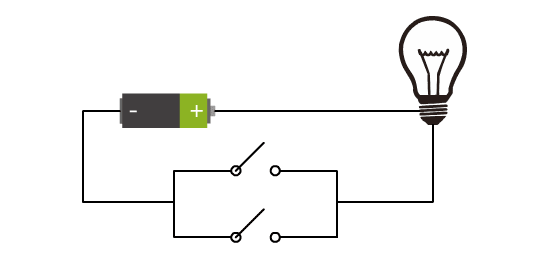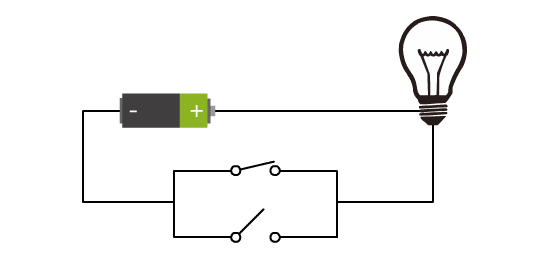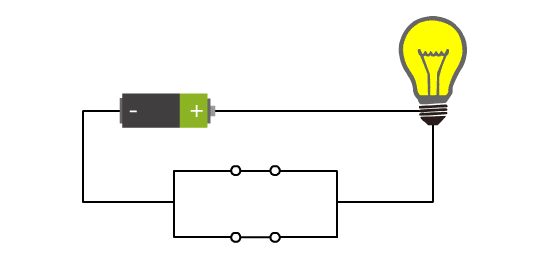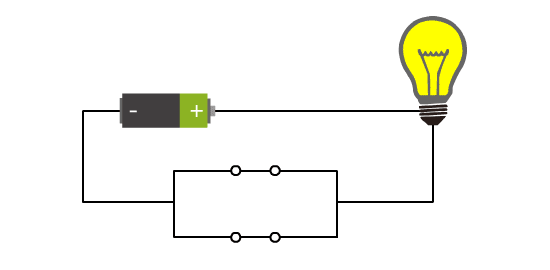
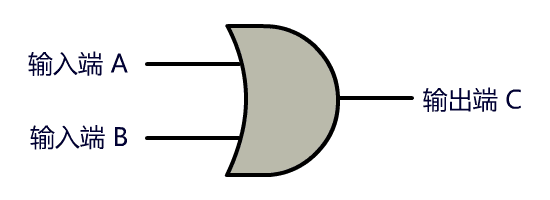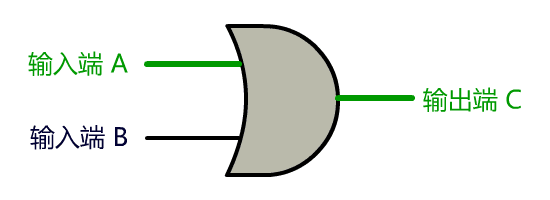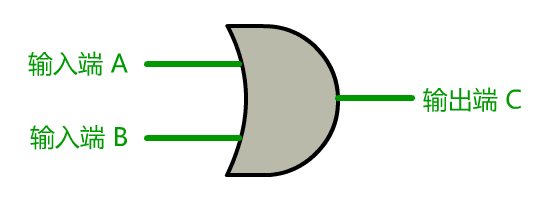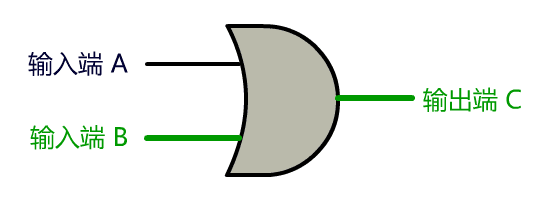
上面这种电路,我把他抽象成如下门电路形状,叫做或门。
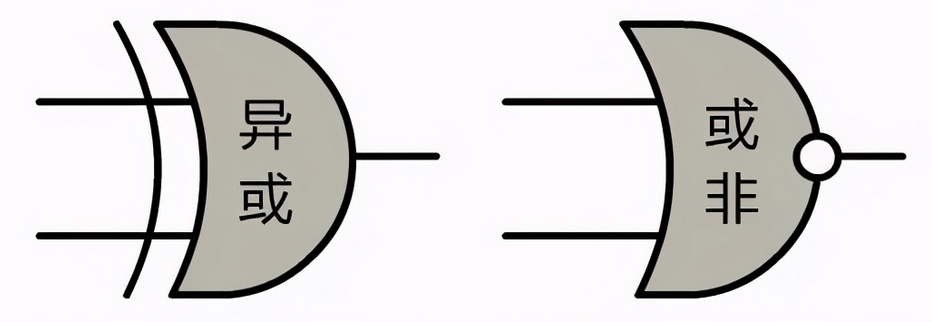
之后便一发不可收拾,我和小宇设计了越来越多的门电路,我们发现,只要是我们能想到的逻辑关系,都可以设计成对应的门电路。
三、加法器——信号的计算
十进制数可以转换成二进制数,而二进制数又可以对应到门电路的输入端与输出端。
于是我和小宇有了一个大胆的想法,能不能设计一个计算加法的电路呢?
我们首先从最简单的一位二进制数相加开始:
0+0=0;0+1=1;1+0=1;1+1=10
变成一张表格如下
加数 A 加数 B 加和输出 进位输出
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
即我们需要设计出一种电路,可以达到表中的输入与输出效果。
经过不懈努力,终于发现这个电路可以由异或门和与门两个门电路组成。
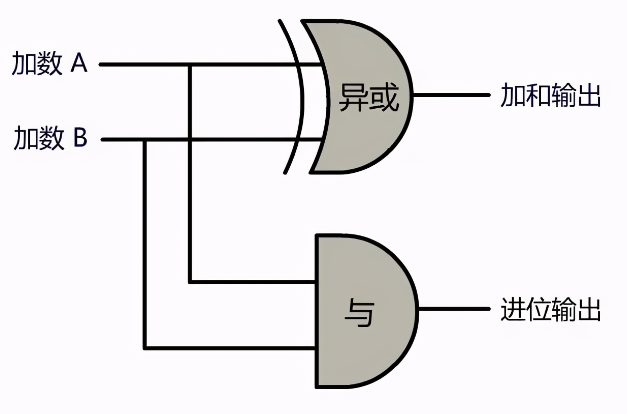
这个装置实现了二进制的一位加法,但它并不完美,因为只考虑了这两个数的进位输出,但没有考虑上一位的进位,所以只能叫半加器。
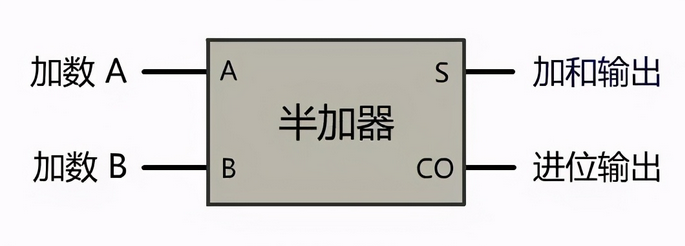
如果将前一个进位考虑进来,只需再多一个半加器,并且拼接一个或门即可(进位输入就是上面计算后的进位,与现在计算后的加和输出相加, 然后计算后的输出就是最后的输出,本次计算后的进位与现在计算后的进位进行或操作,因为是二进制,输出和进位不可能都为1,所以这里使用或操作)。
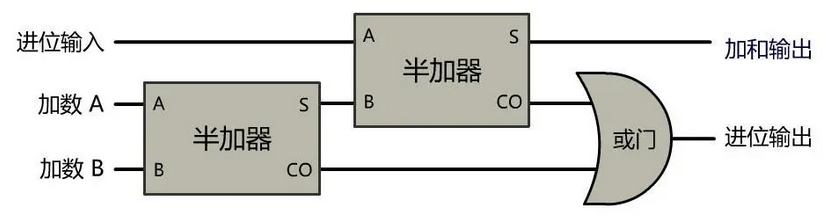
此时我们已经建立好了一个完美的一位加法器,并自豪地称之为全加器。
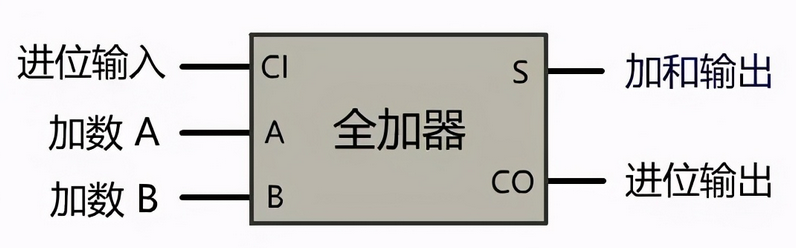
全加器做出来之后,无论多少位的加法器就都可以做出来了,只需将全加器逐个拼起来即可。我们尝试做一个八位加法器。
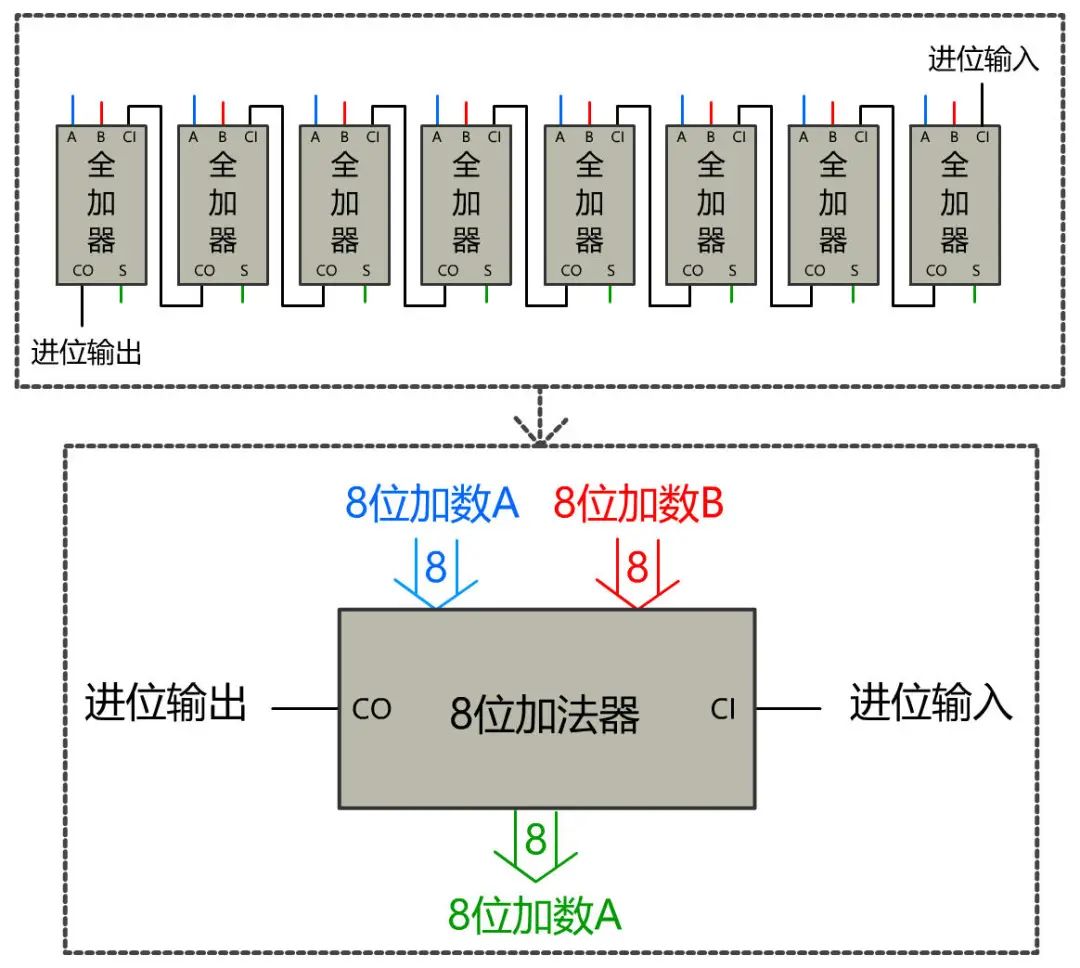
OK,大功告成,有了加法器,理论上就可以实现任何的数学运算了。
因为我们知道乘法可以转换成加法,除法可以转换成减法,而减法又可以转换成补码的加法。现在我们可以自豪地称这个部件为,算术逻辑单元 ALU。

四、时钟——信号的震荡
我和小宇都非常高兴,终于用电路的方式实现了计算功能。
但慢慢的觉得没什么意思了,于是我们又突发奇想,设计了如下诡异的电路。
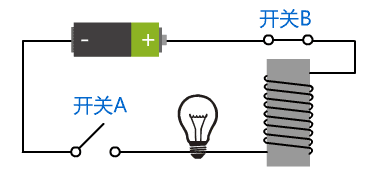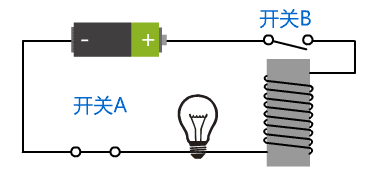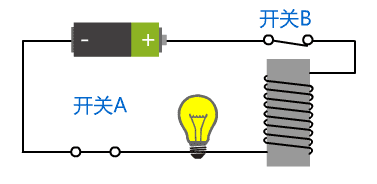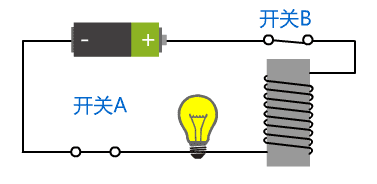
当闭合开关 A 时,整个电路联通,开关 B 将会被吸下来,整个电路断开,电磁铁失去磁性,开关 B 又会弹上去,此时电路又联通,开关 B 又被吸下来。
就这样,开关 B 不断地快速地在开和闭之间循环进行,而我们始终没有去干预这个电路,因此该电路有了自反馈的特性。
由于开关 B 的来回震荡,我们将这种电路称为振荡器,由于它可以产生不断变化的电信号,就像时钟一样不停且规律地跑着, 我们将这个装置又称为时钟。它所产生的交替的电信号称为时钟信号。
五、RAM——保存信号
虽然有了加法器,但是输入的数字从哪里来?能不能先保存在某个地方呢?
我和小宇经过多次实验,发明了一个非常复杂的电路:
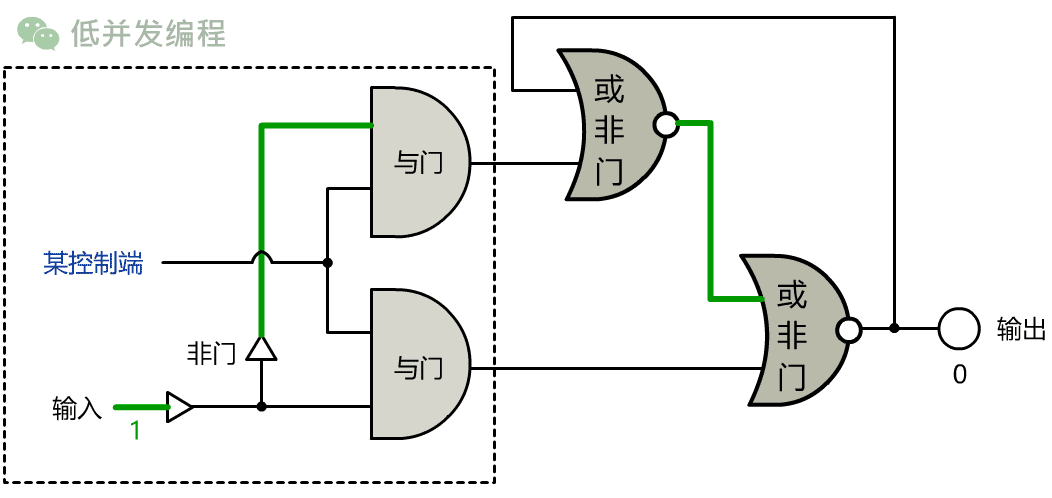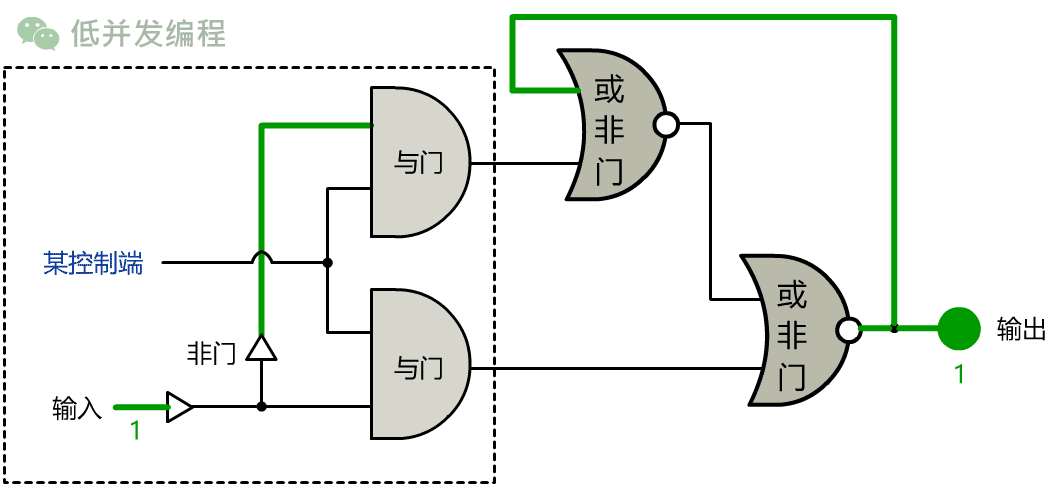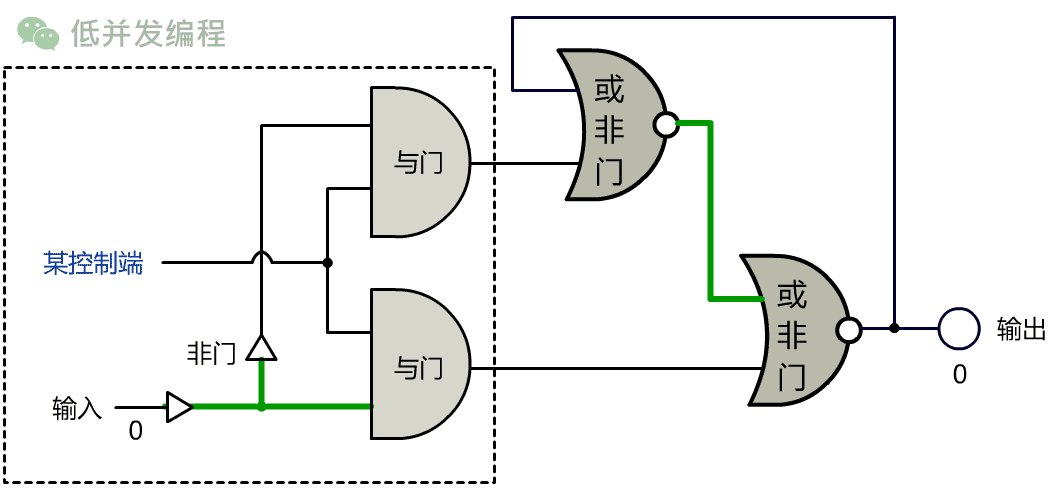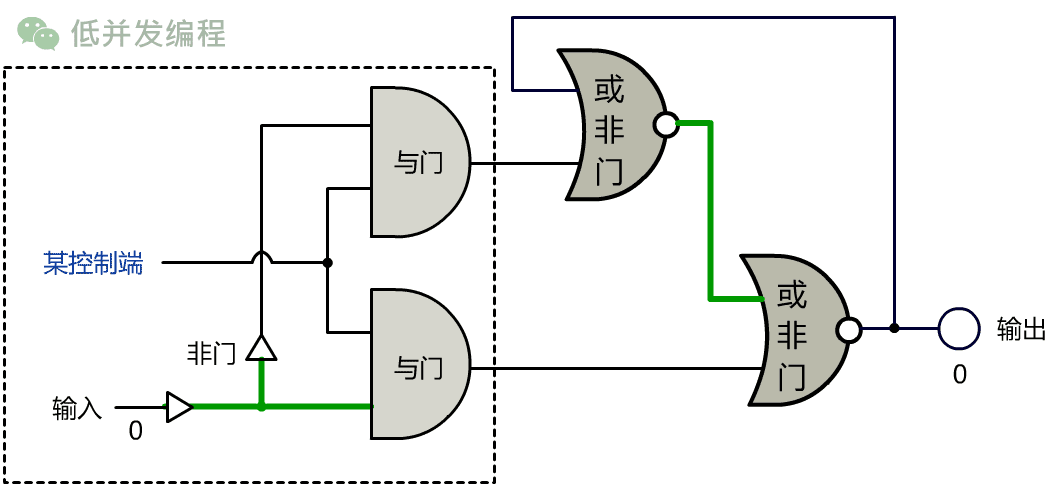
如果输入端为 1,改变”某控制端”信号(信号由 0 变化到 1 这个瞬间),则输出端变为 1,之后输出端仍然保持(存储)着刚刚的 1。
如果输入端为 0,改变”某控制端”信号,则输出端变为 0,之后输出端仍然保持(存储)着刚刚的 0。
如果想不明白也没关系,只要记住这个电路的设计,实现了一位的存储功能!我们叫它 1 位锁存器。
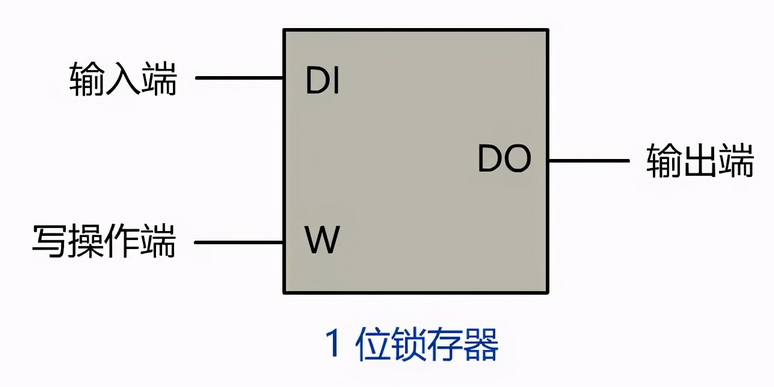
然后我们把多个锁存器组合起来,再加上一些 3-8 译码器,8-1 选择器等电路, 就可以实现一个能保存 8 位二进制的存储器,并且可以随机地读写它, 我们把它叫做 RAM,简称为内存。
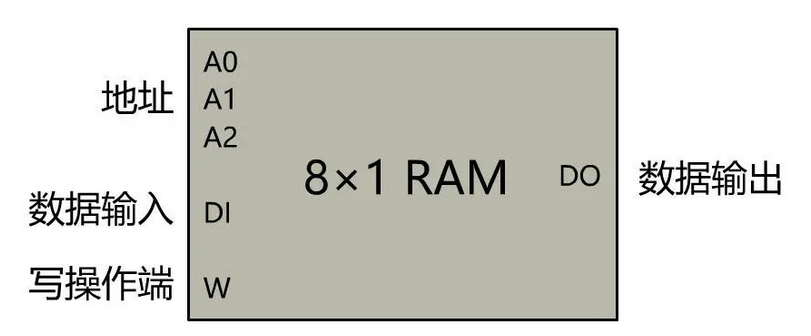
这个组件通过再次组合,可以形成 N × M 的 RAM 阵列。比如我们可以表示一个 1024 * 8 的 RAM 阵列。
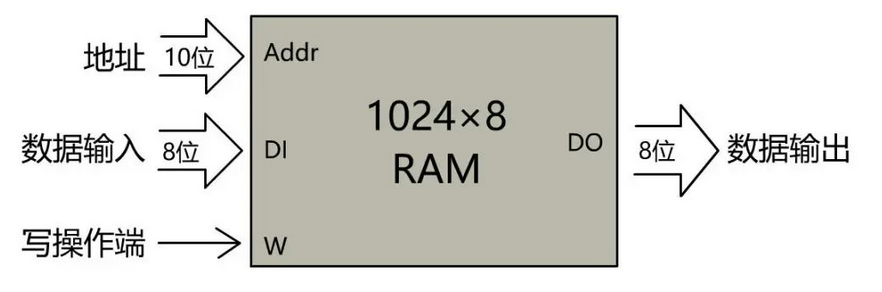
这表示存储容量为 1024 个单位,每个单位占 8 位。
为了更方便地表示,我们规定 1024 = 1K,8 位 = 1 字节(8 bit = 1 byte),那么我们就可以说, 这个 RAM 的存储容量为 1K 个单位,每个单位占 1B。或者说,地址空间为 1K,存储容量是 1KB。
此时这个 RAM 模块已经近乎完美了,我们甚至可以单独对其进行使用,将数据存入某个地址,将某个地址中的数据读出。
怎么方便人操作呢?只需要将地址输入、数据输入、写操作端分别接入一个控制面板,由开关来控制这些信号的输入是 1 还是 0 即可, 然后再将数据输出接入一些灯泡方便观察,这样一个单独的可以手动操作的存储装置,就搞定啦。(下图中有彩蛋~)
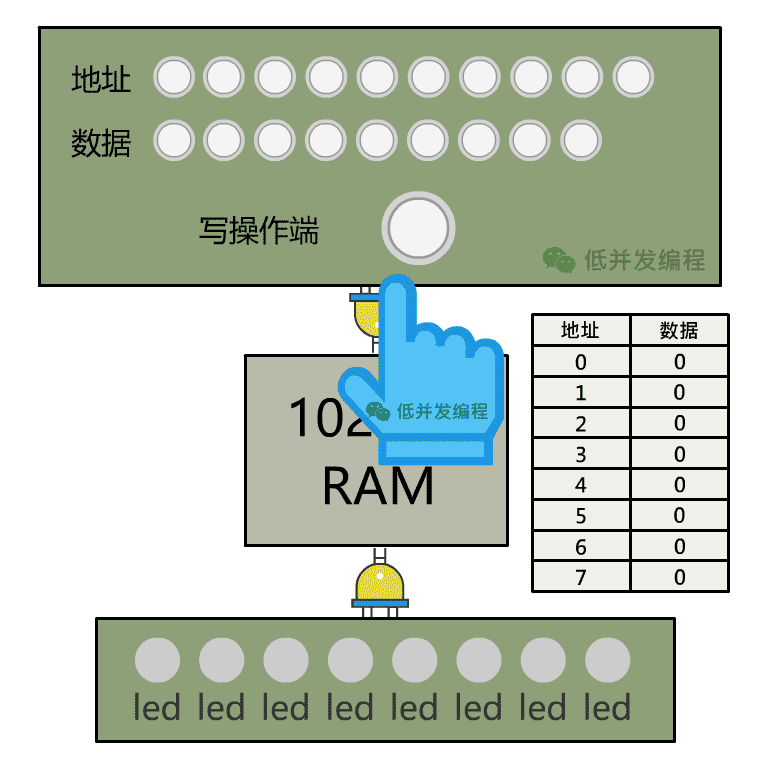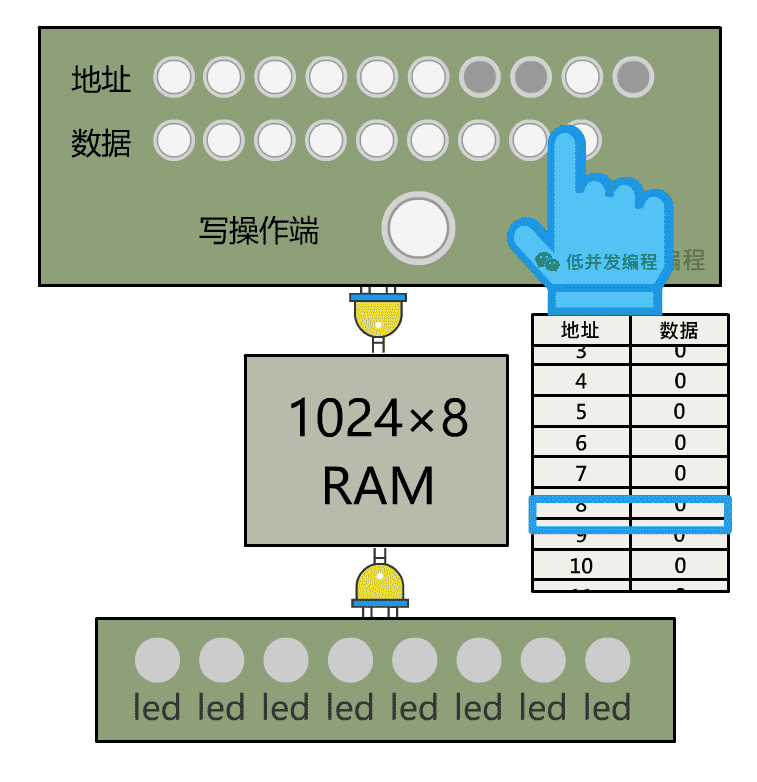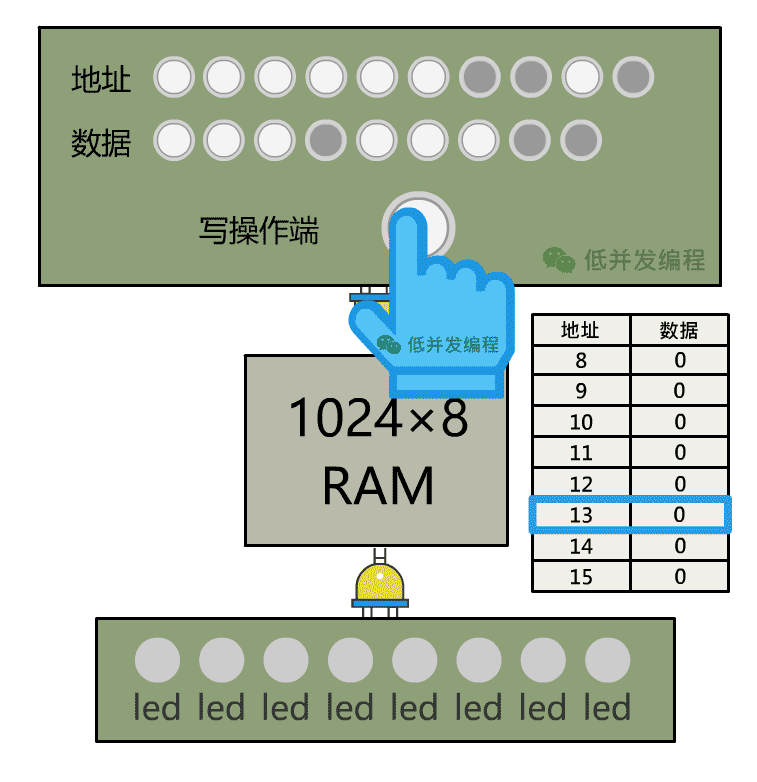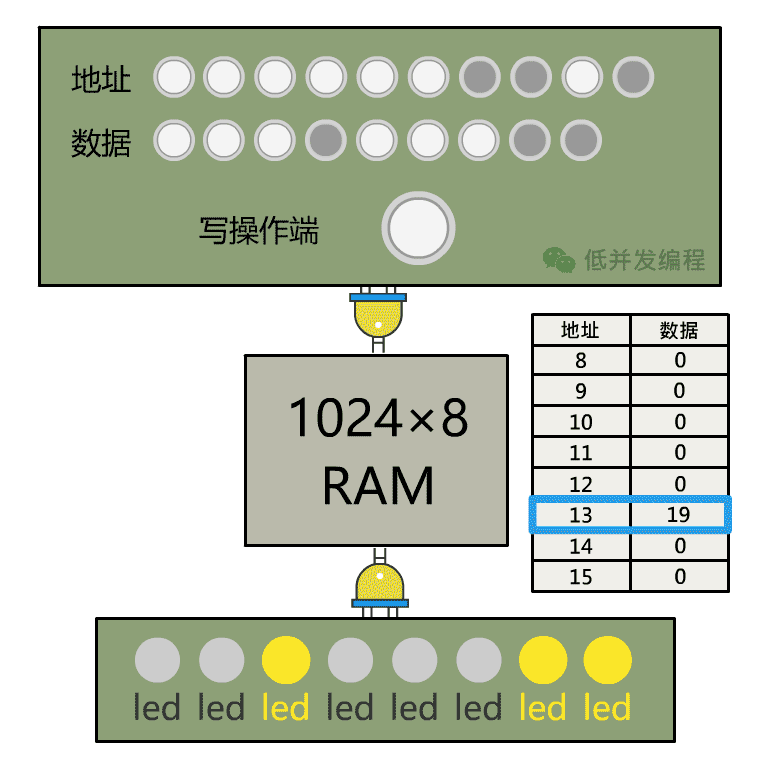
有了可读写的内存,我们就可以事先把几个数字存储内存中了,接下来,我们能否让算术逻辑单元 ALU 自动地读取这个数字,进行加法运算呢?
六、程序——自动化
我们先引入一个新的组件,10 位计数器,这里的 Clk 就接入我们在第四部分讲的时钟信号,Clr 是清零端,具体效果下面动图一目了然。

计数器的输出就是 0,1,2,3,4,5,可以当作内存中的地址。
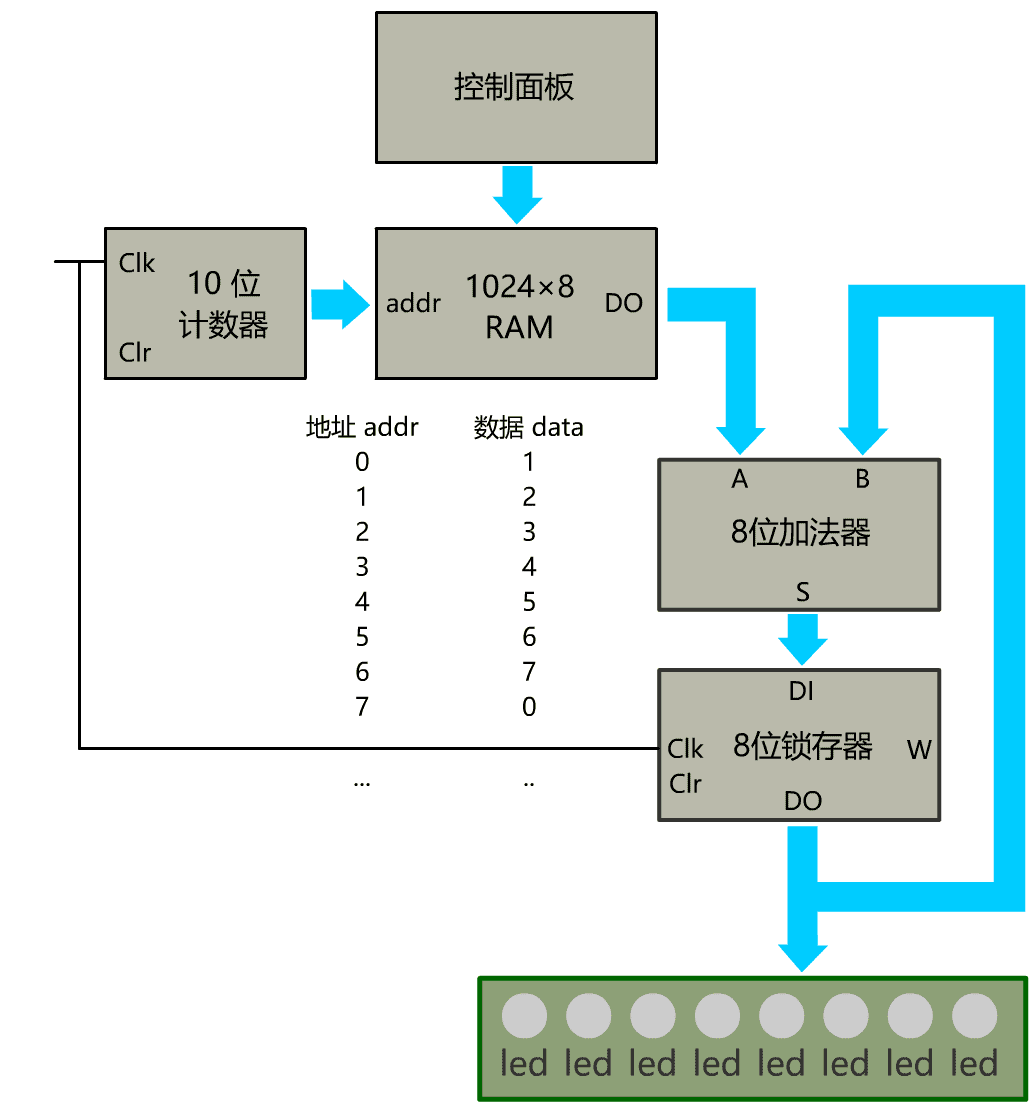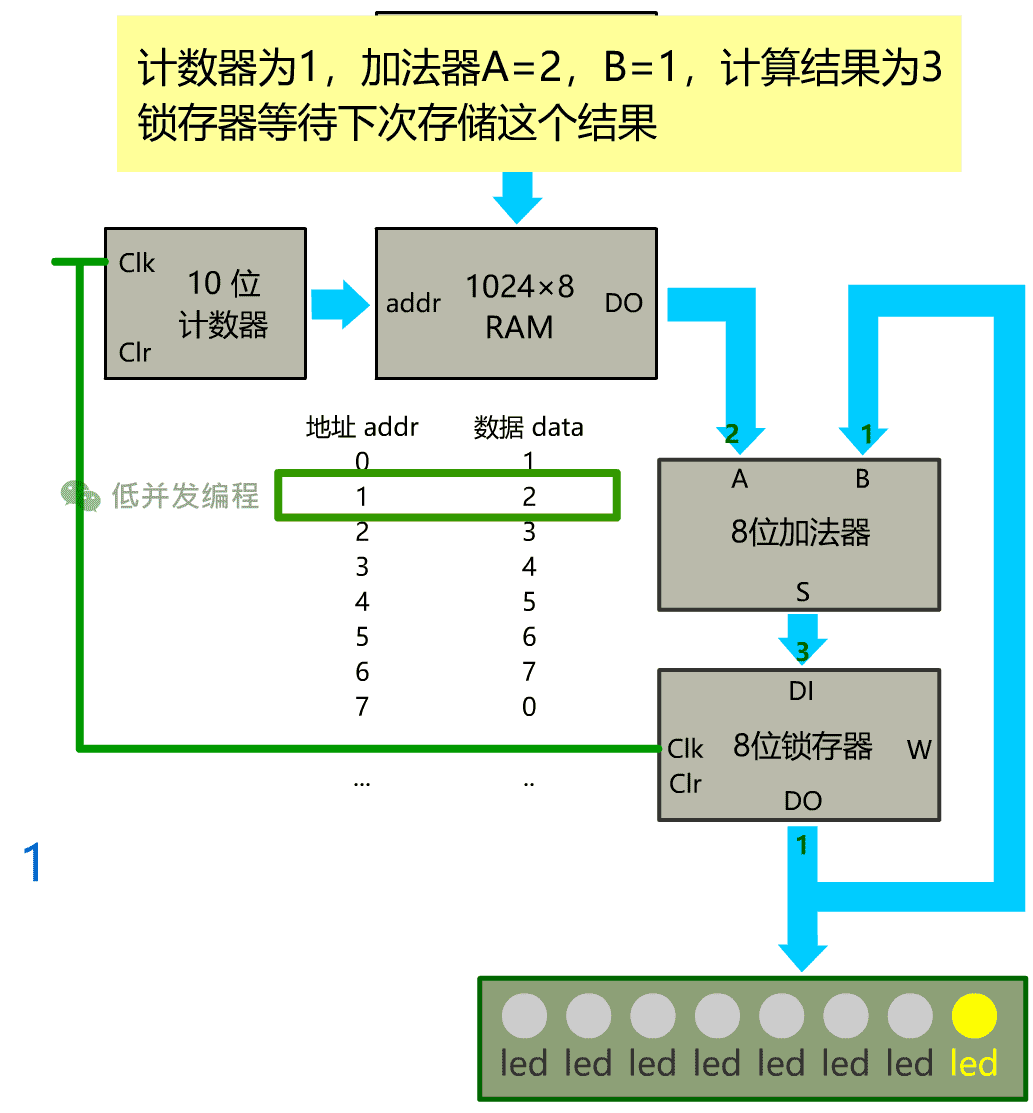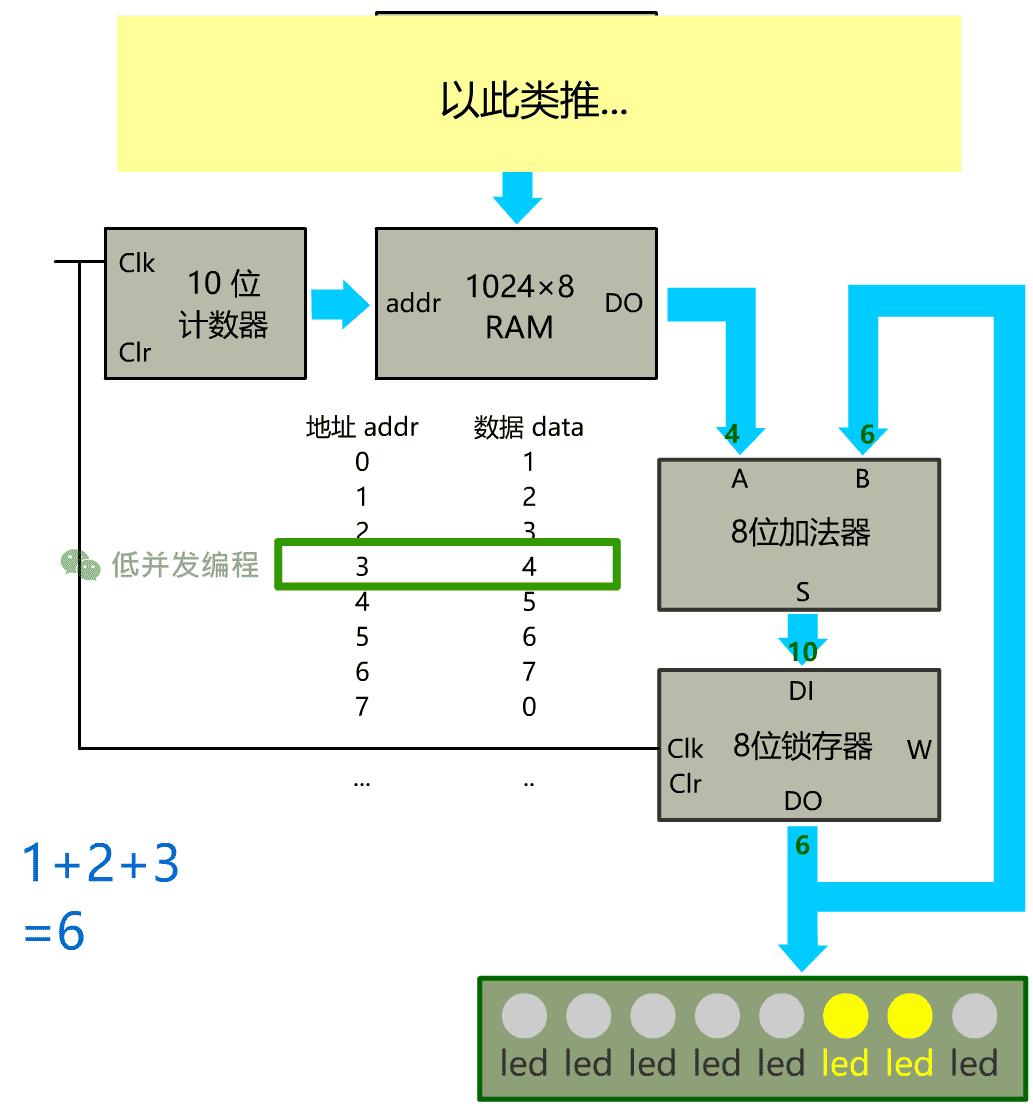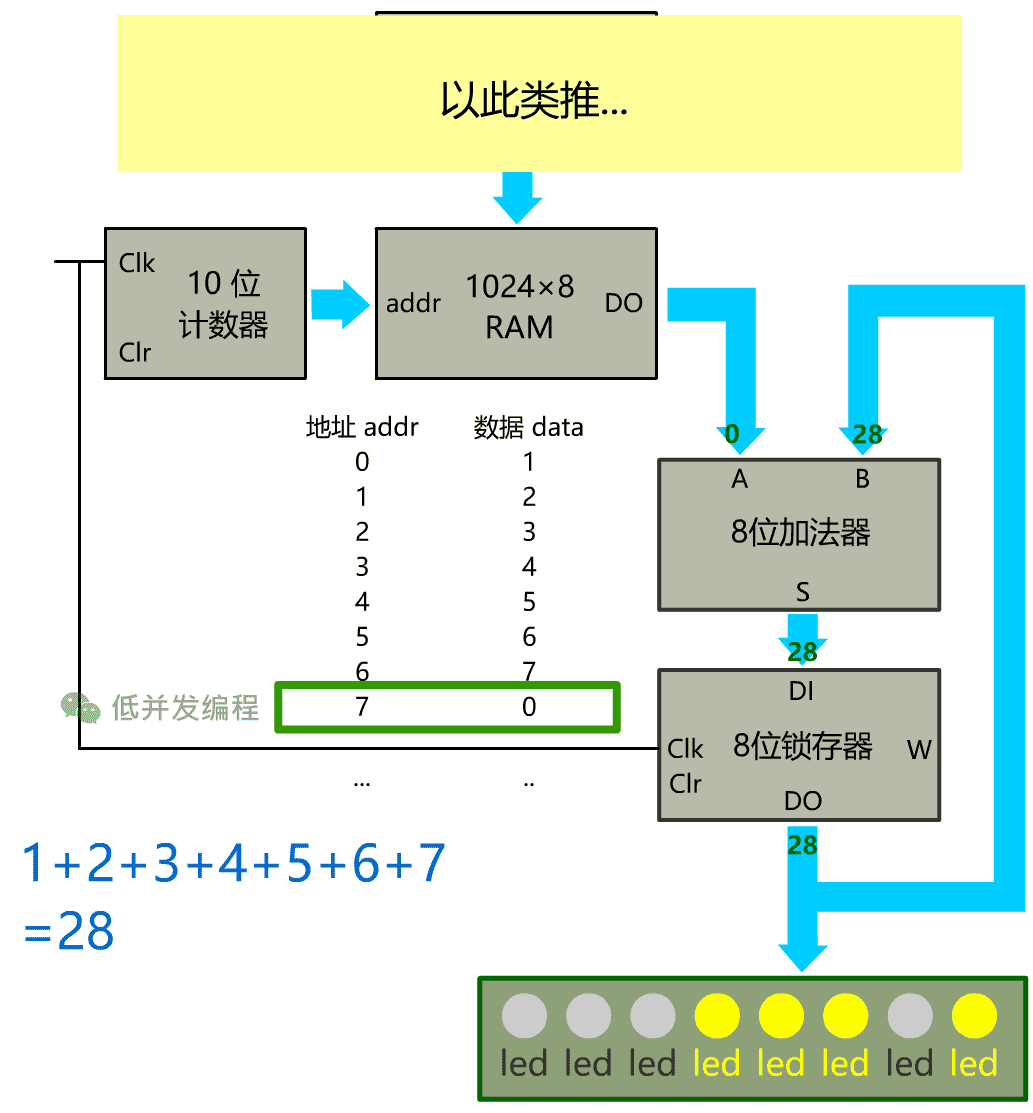
我们把这个计数器,以及上面讲的 ALU 与 RAM 全部连在一起,尝试实现一个可以累积求和的装置。
我们想计算的是 1+2+3+4+5+6+7, 这个自动化的计算器是这么运行的
1、用控制面板在 RAM 的地址 0~6 处存上 1~7 这几个数字的,在上一节已经实现了。
2、当计数器的值是 0 时,数据 1 被输出到加法器进行计算,此时加法器 A=1,B=0,计算结果为 1, 但记住锁存器存储的是上一次的加法器输出 0,这次的计算结果要等下一次锁存器遇到上升沿信号。
3、当计数器的值是 1 时, 数据 2 被输入到加法器,此时锁存器存储了上一次的计算结果 1,并将这个 1 输出给小灯泡, 并同时回传到加法器的B,所以此时加法器 A=2,B=1,计算结果为 3
4、当计数器的值是 3 时,以此类推,请看下图
我们将累加求和这个过程自动化了!之后如果想计算累加和,只需要用控制面板事先在内存里存好数据就可以了!是不是很方便?
七、程序指令
我们还想要更多的自动化!
现在这个装置,只能无脑地将 RAM 中的数据从头到尾一直累加下去,无法选择加哪个不加哪个,也无法选择什么时候停止。
比如我们 RAM 中的数据是这样的。
地址(16 进制) 数据(10进制)
0x00 ...
0x01 10
0x02 ...
0x03 20
0x04 30
0x05 ...
... ...
我们只想让 RAM 蓝色地址处的数据进行累加,其他地方的数据忽略,并且到 RAM 0x05 处就停止,该怎么做呢?
我们可以再增加一个 RAM,这个 RAM 里存放的数据,表示”指令”的含义!
我们先发明三种指令。
add:把 RAM 这个位置处的值进行累加
nop:忽略此处的值(也就是什么都不做)
halt:停止(禁止计数器的值加一)
那么要想达到上述功能,相应的这个指令 RAM 中的数据应该是这样的。
注意:下面指令 RAM 的地址和上面数据 RAM 的地址之间有一一对应关系!
地址(16 进制) 指令RAM的值 指令含义
0x00 nop 什么都不做
0x01 add 累加
0x02 nop 什么都不做
0x03 add 累加
0x04 add 累加
0x05 halt 停止
... ... ...
我们需要引入一个控制单元,放在如下位置。
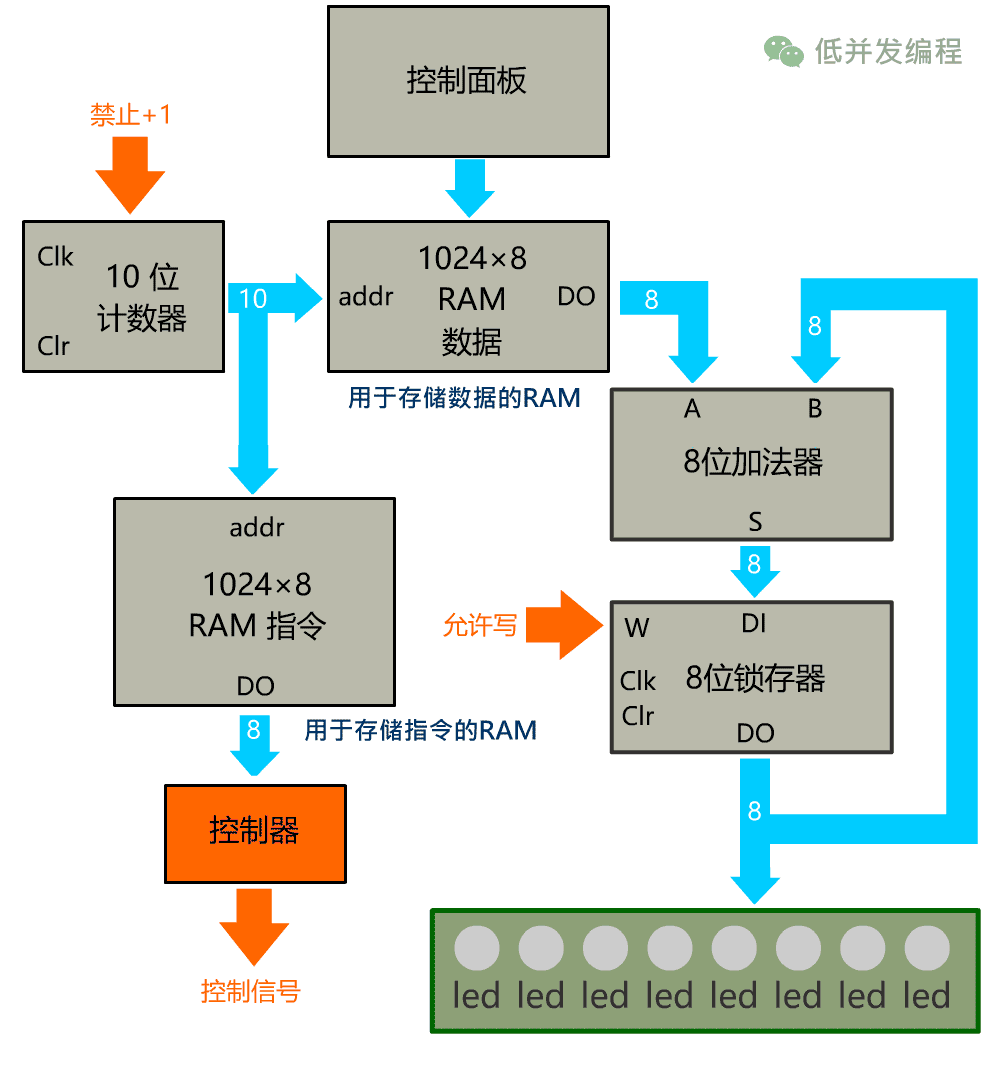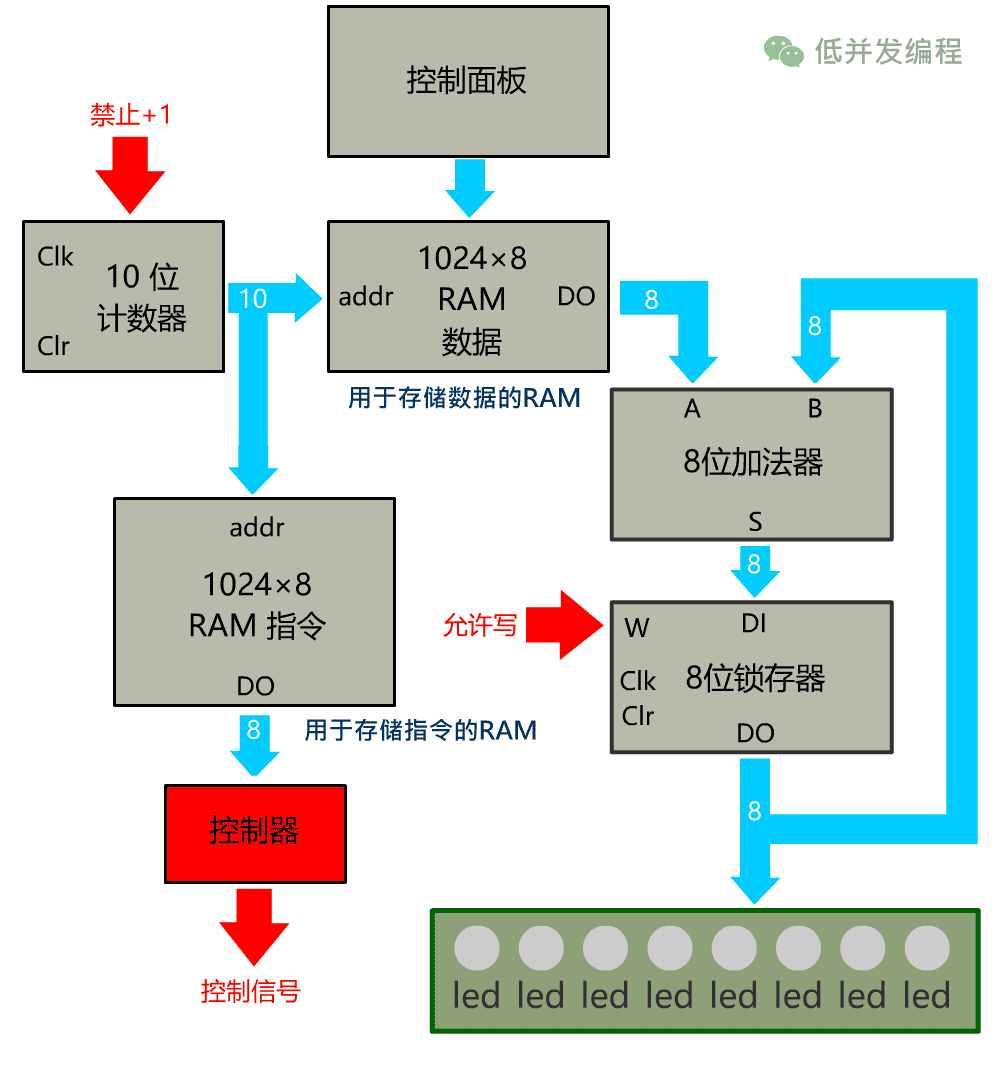
遇到 nop 指令(0x00),那输出就将锁存器的 W 位禁止,不允许锁存器写操作,这样累加结果就不会录入。
再比如遇到输入为 halt 指令(0x05),就将计数器的 EN 位禁止,不允许计数器 +1,这样就达到了停止的效果。
此时再让时钟信号震荡起来,就可以达到有选择地求和过程,并且在指定位置悬停。那现在我们就让时钟信号震动起来,看看这个过程吧。(此处只留关键组件)
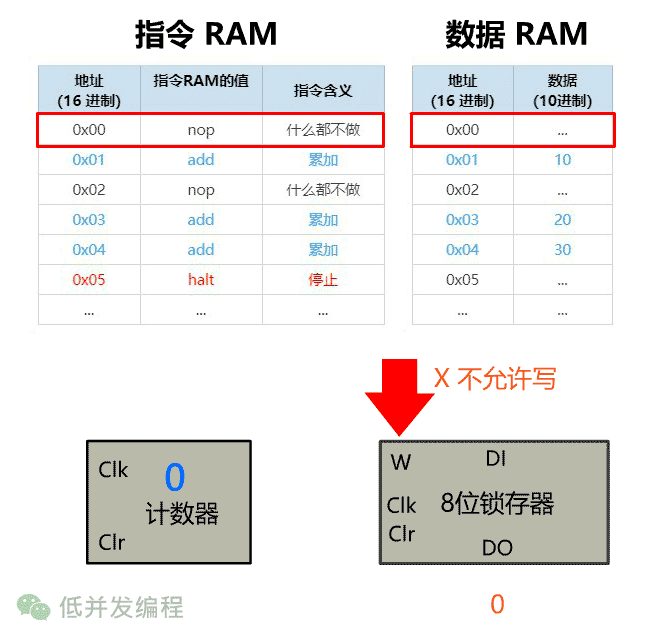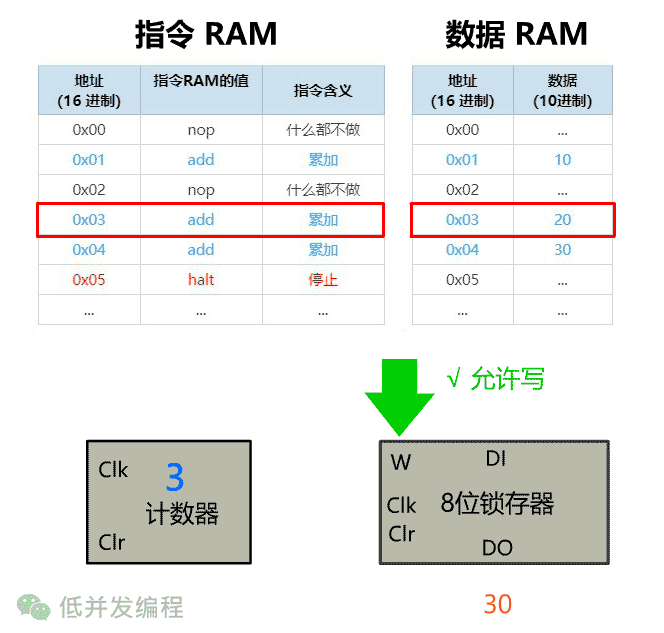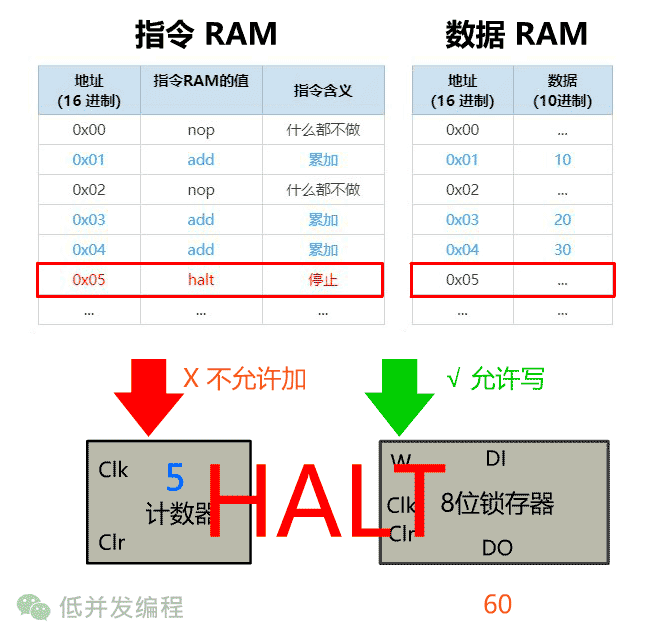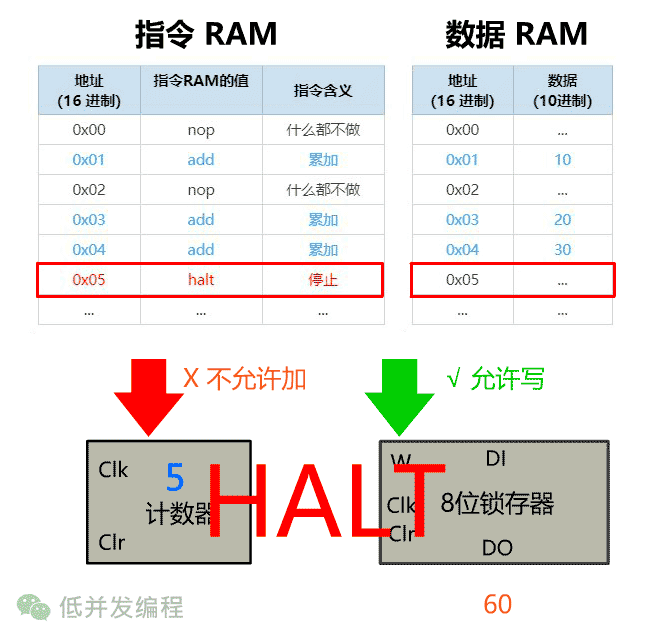
这个控制单元该怎么实现呢?我们知道,只要给出输入,给出输出,任何组件都可以造出来。本文就不再展开了。
有了三个指令,我们知道了通过指令这种方式,配合各种复杂的控制器,即可实现将所有操作统统自动化。
接下来我们需要做的,就是设计控制器,以及约定好一大堆指令,使得通过这一大堆指令的排列组合,可以实现任何自动化的计算操作。
我们将设计好的一大堆指令
称作指令集
我们将指令排列组合后可以实现的功能
称作程序
我们将指令的排列组合这个过程
称作编程
我们将排列组合这些指令的人
称作程序员
而我们将承载这一切的装置,叫做什么呢?
没错,这个破玩意,就是计算机
本文灵感来自一本计算机科普神作,《编码 | 隐匿在计算机软硬件背后的语言》,我在此向这本书致敬。我把核心思想提取出来, 写成了低并发风格的文章,送给各位读者。如果你对计算机对整体原理十分困惑,希望本篇文章可以让你稍稍解惑。 同时希望大家找时间可以将本书通篇阅读,我保证你会很有收获的。 本文和本书的核心目的是让你理解计算机的思想,实际上现在的计算机指令与数据都是放在内存中的, 文中其他地方也都是对计算机的简化模型,且不可出去真的和人家说计算机是个破玩意。
编码:隐匿在计算机软硬件背后的语言
Code:The Hiddden Language of Computer Hardware and Software
第1章 电筒密谈
编码是什么?在本书中,这个词的意思是指一种用来在机器和人之间传递信息的方式。换句话说,编码就是交流。 对任何能听见我们的声音并理解我们所说的语言的人来说,我们发出的声音所形成的词语就是一种编码。 用手电筒能代替声音来与朋友交谈吗?当然值得一试。
第2章 编码与组合
莫尔斯码也被称做二进制码,因为这种编码的组成元素只有两个——“点”和“划”。 不过,点、划的组合却可以表示你想要的任意数目的码字。这其中的规律是什么?本章我们就来探讨一番。
第3章 布莱叶盲文与二元编码
布莱叶盲文是为了便于盲人阅读而发明的一种编码。在这一章中我们将解析布莱叶盲文,来看看它是如何工作的。 我们并不是要真的学习布莱叶盲文,而且也无须刻意记住关于它的什么内容。我们仅仅希望从中归纳出编码的一些性质。
第4章 手电筒剖析
为了理解电在计算机中的工作原理,我们先得仔细钻研一番电学,不过不要担心,只需要一部分基础知识就够了。 在本章,我们将以手电筒为教学道具,引导你走入神秘的电学世界。
第5章 绕过拐弯的通信
在第1章,我们曾经讲过用手电筒与朋友进行交谈的方法,但是这样的方式是有局限性的,你的交流对象必须住在街对过, 而且你们卧室的窗口正好相对。但是,现实不会总是如此。当手电筒的光无法到达朋友的卧室时, 怎样与他们进行无声的交流呢?电路或许可以助你一臂之力。
第6章 发报机与断电器
全球性即时通信对于我们来说已经司空见惯,你要是生活在19世纪早期,可没这么方便。你当然可以进行即时通信或者远距离通信, 但是不能同时做到这两点。即时通信受声音传播距离的限制,或者受视野的限制。使用信件倒是可以进行更远距离的通信, 但是寄信耗费的时间太多,并且需要借助于交通工具。为了解决这个问题,电报应运, 而生而伴随着电报诞生的继电器更是具有重要意义的伟大发明。
第7章 十进制记数法
人们很容易理解,语言只不过是一种编码。比如英文中的“cat”(猫)在其他语言中可以写做gato、chat、Katze、KOIIIK或kátta。 然而,数字似乎并不是那么容易随文化的不同而改变。不论我们说什么语言,或使用什么样的发音, 在这个星球上的所有人都用以下方式来书写数字:0,1,2,3,4,5,6,7,8,9。你了解这十个数字么?
第8章 其他进位制记数法
对于人类而言,10是一个非常重要的数字。它是我们大多数人拥有的手指或脚趾的数目。我们人类已经适应了以10为基数的数字系统。 但是只能使用十进制来计数吗?如果人类像卡通人物那样每只手只有4根手指会怎样?
第9章 二进制数
二进制是最简单的数字系统,其中只包含两个数字:0和1。二进制中的1位(bit)称为1比特,我们可以用它来表达简单的信息: 是或不是;亮或灭;打开或关闭,等等。而事实上只要信息能转换成两种或多种可能性的选择,就都可以用比特来表示。 这种例子在日常 生活中随处可见,比如照相机胶卷的胶片速度,各种商品包装上的条形码。
第10章 逻辑与开关
对于古希腊人而言,逻辑是在追求真理的过程中所使用的一种分析方法,是一种哲学形式。 而英国的数学家乔治布尔却认为可以找到一种数学形式来描述逻辑,因此他发明了布尔代数。 更重要的是,布尔代数运算可以用开关、导线和灯泡组成的电路来实现,布尔代数中的AND和OR, 与线路中开关的串联和并联,有着奇妙的对应关系。
第11章 逻辑门电路
继电器像开关一样,可以串联或并联在电路中执行简单的逻辑任务。这种继电器的组合叫做逻辑门(logic gate),也简称门。 这里提到的逻辑门执行“简单”逻辑任务是指逻辑门只完成最基本的功能。本章就介绍那些用以完成最基本逻辑任务的门。
第12章 二进制加法机
加法是算术计算中最基础的运算,如果想搭建一台计算机的话,首先就要搭建出计算两个数加和的器件。 本章我们将利用前面的章节中用过的开关、灯泡、导线、电池、逻辑门等这些简单的元件,搭建一个二进制加法器。
第13章 如何实现减法
当你确信继电器连接在一起真的可以实现二进制数加法的时候,你可能会问:“如何实现减法呢?”问得好! 这表明你是相当有觉察力的,加法和减法在某些方面互相补充,但是在机制上二者却存在本质区别。 不过,没关系,我们可以想一些办法,把减法运算变成加法。
第14章 反馈与触发器
想象一下,如果你没有了记忆力,该如何去数数?我们不记得刚刚数过的数,当然也就无法确定下一个数是什么! 同理,一个能计数的电路必定需要触发器。本章要介绍的就是各种触发器。
第15章 字节与十六进制
在前面的章节中,加法器、锁存器以及数据选择器的输入和输出形式都是8位的数据流,也即数据路径的位宽为8, 为什么要定义为8位呢?为什么不是6位、7位、9位或10位?本章就要解释其中的缘由。
第16章 存储器组织
每天清晨,我们将自己从沉睡中唤醒,这时大脑的空白会很快被记忆填满。我们立刻会意识到自己身在何方, 最近做了些什么事情,有什么计划打算。有的事情我们很快就能想起来,但有时并非如此。 我们可以借助许多工具来记录信息,比如笔和纸、磁带,当然现在还可以使用存储器。
第17章 自动操作
人类的本性中带有一些懒惰的特质。我们总是抵触繁重的工作,对枯燥的、重复性的工作深恶痛绝。 所以,当你必须用前面搭建的加法器计算100个数,甚至更多个数的加法时,有一种念头就会不可遏制地从脑子里冒出来: 怎样让加法器自动地完成数据输入和计算呢?办法肯定是有的,那就是编写程序。
第18章 从算盘到芯片
算盘、滑尺、纳皮尔骨架、差分机、解析机、继电器、电子管、晶体管、芯片、计算机; 甘特、帕斯卡、莱布尼兹、杰奎德、巴贝芝、图灵、冯诺依曼、香农;IBM、贝尔实验室……你觉得应接不暇了吗? 把这些你或者熟悉或者生疏的名词和名字串起来,就是人类的计算工具发展史。让时光倒流,去看看那些精巧的工具,感受天才们的巧思吧!
第19章 两种典型的微处理器
将中央处理器的所有构成组件封装到一块硅芯片上,就得到了微处理器。第一片微处理器芯片诞生于1971年, 即Intel 4004系列,其中集成了2300个晶体管,你或许觉得可笑——如今家用计算机的微处理器上所安置的晶体管数量已经以亿为计量单位了。 但是,从本质上来说,微处理器实际所做的工作并没有变。在本章,我们就来看看两种有着辉煌历史的典型微处理器:Intel 8080和Motorola 6800。
第20章 ASCII码和字符映射
计算机中的存储器唯一可以存储的形式是比特,因此如果想在计算机上处理信息,就必须把它们转换为比特的形式来存储。 我们已经掌握了如何用比特来表示数字和机器码。如何用它来存储文本呢?毕竟,人类所积累的大部分信息, 都以各种文本形式保存的。下面就轮到ASCII码出场了!
第21章 总线连接
一台计算机包括很多部件:中央处理器、存储器、输入/输出设备等。通常这些部件按照功能被分别安装在两个或更多的电路板上。 这些电路板之间通过总线(bus)通信。如果对总线做一个简单的概括,可以认为总线就是数字信号的集合, 而这些信号被提供给计算机上的每块电路板。
第22章 操作系统
你或许梦想过自己组装一台近乎完整的计算机,像老木偶匠盖比特雕刻木偶匹诺曹一样,全部亲自动手用小零件完成。 不过在你的机器能完成你想要的操作之前,还差一个重要的东西——操作系统!
第23章 定点数和浮点数
整数、分数以及百分数等各种类型的数字与我们形影不离,它几乎出现在我们生活的所有角落。 例如你加班2.75小时,而公司按正常工作时间的1.5倍支付你工资,你用这些钱买了半盒鸡蛋并交了8.25%的销售税。 在计算机的内存里,所有的数都表示为二进制形式。通过前面的学习,我们知道2用二进制可以表示为102, 可是2.75用二进制怎样表示呢?这就是本章的主题。
第24章 高级语言和低级语言
第22章介绍了如何编写一段简单的程序,让我们可以利用键盘将十六进制机器码输入计算机,以及通过视频显示设备来检查这些代码。 但是使用机器码编写程序就如同用牙签吃东西,伸出手臂费半天劲刺向食物,但每次都只获取到小小的一块, 用这种低级语言编写程序既费力又费时,有悖于我们发明计算机的初衷。 不过,人们想出了一种效率更高的编程方法——使用高级语言。
第25章 图形化革命
回顾历史,从第一台继电器计算器出现到现在为止,六七十年过去了,计算机的处理速度飞速增长。 不过要充分利用计算机日益增长的运算和处理能力,就必须不断改进计算机系统中的用户接口(User Interface), 因为它是人机交互的轴心。图形化革命来了!
附原书
https://ibaiyang.github.io/blog/books/编码:隐匿在计算机软硬件背后的语言.pdf
参考资料
《编码:隐匿在计算机软硬件背后的语言》
图解 你管这破玩意叫计算机? https://www.cnblogs.com/flashsun/p/14401623.html
你管这破玩意叫 CPU ? https://mp.weixin.qq.com/s/4yiA5NUjHZlphkQjtNhOWQ
假如你来发明编程语言 https://mp.weixin.qq.com/s/mn5mAD70SnHKlX9MUyesUA