正文
数组的类型定义
一维数组
#include <stdio.h>
int main ()
{
int n[ 10 ]; /* n 是一个包含 10 个整数的数组 */
int i,j;
/* 初始化数组元素 */
for ( i = 0; i < 10; i++ )
{
n[ i ] = i + 100; /* 设置元素 i 为 i + 100 */
}
/* 输出数组中每个元素的值 */
for (j = 0; j < 10; j++ )
{
printf("Element[%d] = %d\n", j, n[j] );
}
return 0;
}
二维数组
a_mn 受到行和列两个关系的约束:第i行的行向量,第j列的列向量
设数组开始存放位置 , LOC(0,0) = a, 每个元素占用x个存储单元,每一行n的元素,每一列m个元素。则LOC(i, j)在内存中的位置,
行优先的情况:
LOC(i, j) = a + (i * n + j) * x
列优先的情况:
LOC(i, j) = a + (j * m + i) * x
数组的顺序表示和实现
矩阵的压缩存储
在数值分析中经常出现一些阶数很高的矩阵,同时在矩阵中有许多值相同的元素,或者是零元素。 有时为了节省存储空间,可以对这类矩阵进行压缩存储。
假若值相同的元素或者零元素在矩阵中是分布有一定规律,则我们称此类矩阵为特殊矩阵; 反之,称为稀疏矩阵
对称矩阵的压缩存储
设有一个n*n的对称矩阵A。
a00 a01 a02 …… a0n−1
A = a10 a11 a12 …… a1n−1
a20 a21 a22 …… a2n−1
a30 a31 a32 …… a3n−1
在矩阵中,aij = aji
- 例题4-1 对特殊矩阵采用压缩存储的主要⽬的是()。
A.表达变得简单 B.对矩阵元素的存取变得简单 C.去掉矩阵中的多余元素 D.减少不必要的存储空间
数组的顺序存储结构
为节约存储空间,只存对角线及对角线以上的元素,或者只存对角线及对角线以下的元素。前者称为上三角矩阵,后者称为下三角矩阵。
把他们按行存放于一个一维数组B中,称之为对称矩阵A的压缩存储方式。
数组B共有: n + (n − 1) + (n − 2) + …… + 1 = n * (n + 1)/2 个元素
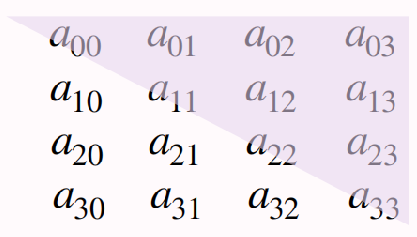
上三角矩阵: 若i>j,数组元素A[i][j]在数组中的存放位置为
1 + 2 + 3 + . . . + j + i = (j + 1) * j/2 + i
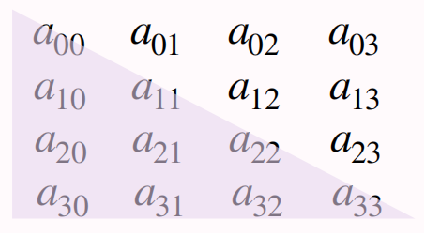
下三角矩阵: 若i<j,数组元素A[i][j]在数组中的存放位置为
1 + 2 + 3 + . . . + i + j = (i + 1) * i/2 + j
- 例题4-2
若将n阶上三角矩阵A按列优先级压缩存放在一维数组B[1…n (n+1)/2+1]中,
则存放到B[k]中的非零元素ai,j(1 < = i, j < = n)的下标i,j与k的对应关系是()。
A. i(i+1)/2+j B.i(i-1)/2+j-1 C. j(j-1)/2+i D.j(j-1)/2+i-1
- 例题4-3
若将n阶下三角矩阵A按列优先级压缩存放在一维数组B[1…n (n+1)/2+1]中,
则存放到B[k]中的非零元素ai,j(1 < = i, j < = n)的下标i,j与k的对应关系是()。
A. (j-1)(2n-j+1)/2+i-j B.(j-1)(2n-j+2)/2+i-j+1 C. (j-1)(2n-j+2)/2+i -j D.(j-1)(2n-j+1)/2+i-j-1
三对角矩阵的压缩存储
三对角矩阵中除主对角线及在主对角线上下最邻近的两条对角线上的元素外,所有其他元素均为0。总共有3n-2个非零元素。

稀疏矩阵的压缩存储
稀疏矩阵
非零元素个数远远少于矩阵元素个数且分布无规律可循。
0 0 0 2 0
0 9 11 2 0
A5*6 = 1 0 0 0 0
15 0 0 0 3
0 0 0 0 0
0 22 -7 0 0
行(row) 列(col) 值(value)
0 3 2
1 1 9
1 2 11
2 0 1
3 0 15
3 4 3
5 1 22
5 2 -7
稀疏矩阵转置算法思想
一个稀疏矩阵的转置仍然是一个稀疏矩阵。
- 矩阵的行列值交换。
- 将每一个三元组的i和j相互调换。
- 重排三元组直接的次序

- 例题4-4
将对三角矩阵A[1…100][1…100]按行优先存⼊一维数组B[1…298]中,A中元素A[66][65]在数组B中的位置K为()。
A. 198 B.195 C. 197 D.196
例题解析
- 解析4-1 D
由于特殊矩阵中含有很多相同的元素或零元素。故可以给相同的元素只分配一次存储空间,从⽽达到节省内存的⽬的。
- 解析4-2 C
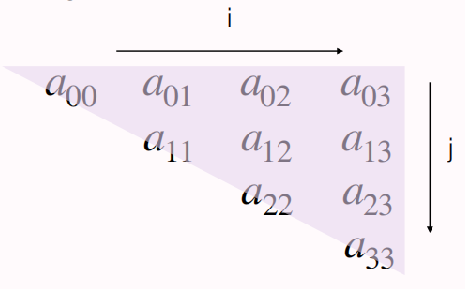
在B[k]的前面有j-1列,由等差数列1+2+3+…+j-1=j (j-1)/2个元素,元素a[i,j]在第j列上是第i个元素,
注意到数组的下标是从1开始的,因此k=j(j-1)/2+i
- 解析4-3 B
在B[k]的前面有j-1列,由等差数列n+(n-1)+…+(n-j+2)=(j-1)(2n-j+2)/2个元素,元素a[i,j]在第j列上是第i-j+1个元素,
注意到数组的下标是从1开始的,因此加在一起,选B。
- 解析4-4 B
对于三角矩阵,将A[1…n][1…n]压缩至B[1,3n-2]时,k与i,j的对应关系应是k=2i+j-2,
则A中的元素A[66][65]在数组B中的位置k为2*66+65-2=195。