数据结构不挂科 3 栈和队列

正文
参考资料

正文

模块1 栈

⼩节1 栈的类型定义

栈的定义

也称为堆栈，是一种先进后出，删除和插⼊都在栈顶操作的线性表。

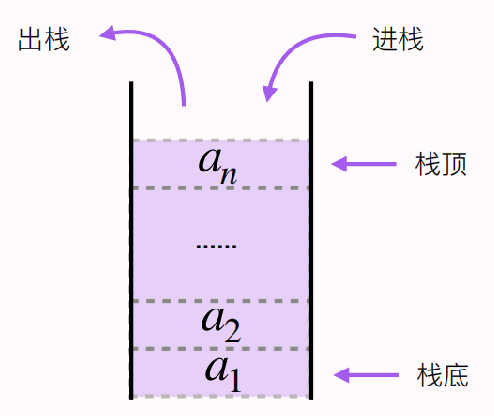
栈的插入

push()：在栈顶插⼊元素。

栈的删除

pop()：在栈顶移除一个元素，并将栈数-1。

例题3-1

若元素a,b,c,d,e,f依次进栈，允许进栈、退栈操作交替进行，但不允许连续三次进行退栈工作，则不可能得到的出栈序列是().

A．dcebfa B．cbdaef C．dbcaef D．afedcb

栈的基本操作

InitStack(&S) 
DestroyStack(&S) 
StackLength(S) 
StackEmpty(S) 
GetTop(S,&e) 
ClearStack(&S) 
Push(&S,e) 
Pop(&S,&e) 
StackTravers(S,visit())

InitStack(&S) 操作结果：构造一个空栈S。

void Init(SqStack s)
{
    s.base = (int *)malloc(size*sizeof(int));
    s.top = s.base;
    s.stacksize = size;
}

Push（&S，e） 初始条件：栈S已存在操作结果：插⼊元素e为新的栈顶元素

void push(SqStack s,ini e)
{
    if (s.top - s.base > s.stacksize) {
        s.base = (int*)realloc(s.base, (s.stacksize + incresize) * sizeof(int));
        s.top = s.base + s,stacksize;
        s.stacksize += incresize;
    }
    
    *s.top ++= e;
}

Pop(&S，&e) 初始条件：栈S已存在且非空。操作结果：删除S 的栈顶元素，并用e返回其值

void pop(SqStack s,ini e)
{
    if (s.top != s.base) {
        e = *(--s.top);
    }
    
    count<<e<<endl;
}

打印函数：

void Print(SqStack *s)
{
    int *temp;
    temp = s->top;
    while(temp != s->base)
    {
        temp--;
        printf("%d ", *temp);
    }
}

⼩节2 栈的应用举例

数制转换

算法原理：

N = (N div d)×d + N mod d

⼗进制转⼋进制: (1348)10 = (2504)8

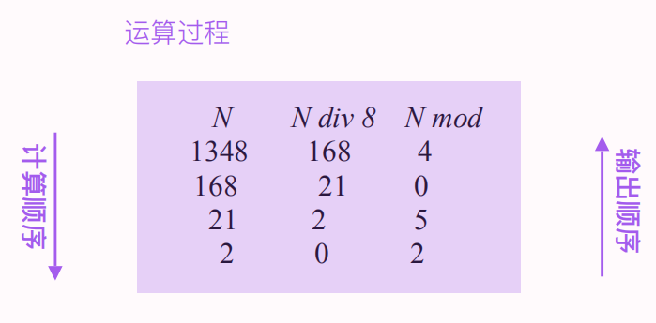
代码实现：

void conversion() {
    InitStack(S);
    scanf("%d", N);
    while (N) {
        Push(S, N % 8);
        N = N / 8;
    }
    
    while (!StackEmpty(S)) {
        Pop(S, e);
        printf("%d", e);
    }
}

2    <---- 栈顶
5
0
4

括号匹配的检验

[ ( [ ] [ ] ) ]
1 2 3 4 5 6 7 8

检验括号是否匹配的方法可用 “期待的急迫程度”这个概念来描述。

出现不匹配的三种可能情况：

1.到来的右括弧不是所“期待”的；

2.到来的是“不速之客”；

3.直到结束，也没有到来所“期待”的括弧；

1.凡出现左括弧，则进栈；
2.凡出现右括弧，⾸先检查栈是否为空
若栈空，则表明该“右括弧”多余
否则和栈顶元素比较
若相匹配，则“左括弧出栈” 
否则表明不匹配；
3.表达式检验结束时，
若栈空，则表明表达式中匹配正确，
否则表明“左括弧”有余；

表达式求值

表达式的三种标识方法:

Exp = S1 + OP + S2

前缀表示法：OP+S1+S2

中缀表示法：S1+OP+S2

后缀表示法：S1+S2+OP

表达式求值举例

Exp = a × b + (c − d / e) × f
前缀式: + × a b × − c / d e f
中缀式: a × b + c − d / e × f
后缀式: a b × c d e / − f × +

后缀式求值

先找运算符，再找操作数

ab × cde/ − f × +
a×b 
     d/e
     c − d/e
     (c − d/e) × f
= (a × b) + (c − d/e) × f 

例题3-2 表达式a*(b+c)-d的后缀表达式是

A.abcd*+- B. abc+*d- C. abc*+d- D. -+*abcd

栈的递归调用

递归函数：一个直接调用⾃⼰或通过一系列的调用语句间接地调用⾃⼰的函数。

#include <stdio.h>
int f(int m)
{
    if (m == 1) {
        return 1;
    } else {
        printf("m = %d\n", m);
        return f(m - 1);
    }
}

int main()
{
    int n;
    int f(int m);
    printf("请输入一个大于1的数：");
    scanf("%d", &n);
    printf("%d\n", f(n));
    return 0;
}

⼩节3 栈类型的实现

顺序栈

类似于线性表的顺序映象实现，指向表尾的指针可以作为栈顶指针。

栈的顺序存储表示：

#define STACK_INIT_SIZE 100
typedef struct {
    SElemType *base;
    SElemType *top;
    int stacksize;
} SqStack;

构造一个最大空间为 maxsize 的空顺序栈 S：

Status InitStack (SqStack &S, int maxsize)
{
    s.base = new ElemType[maxsize];
    if (!S.base) {
        exit(OVERFLOW);  // 存储分配失败
    }
    S.top = S.base;
    S.stacksize = maxsize;
    return OK;
}

顺序栈的基本操作：

Status Push (SqStack &S, ElenType e)
{
    // 若栈不满，则将e插入栈顶
    if (S.top - S.base >= S.stacksize) {
        // 栈满
        return OVERFLOW;
    }
    *S.top++ = e;
    return ok;
}

Status Pop (SqStack &S, ElenType &e)
{
    // 若栈不空，则删除S的栈顶元素，
    // 用e返回其值，并返回ok，
    // 否则返回失败
    if (S.top == S.base) {
        return ERROR;
    }
    e = *--S.top;
    return ok;
}

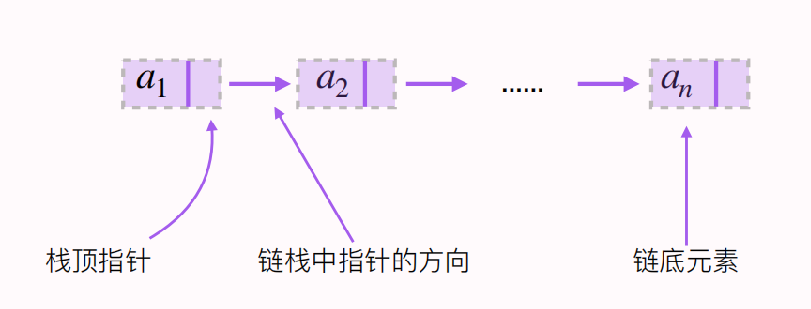
链栈

线性表有顺序存储结构和链式存储结构，栈属于线性表的一种，也具有顺序存储结构和链式存储结构。

模块2 队列

⼩节1 队列的类型定义

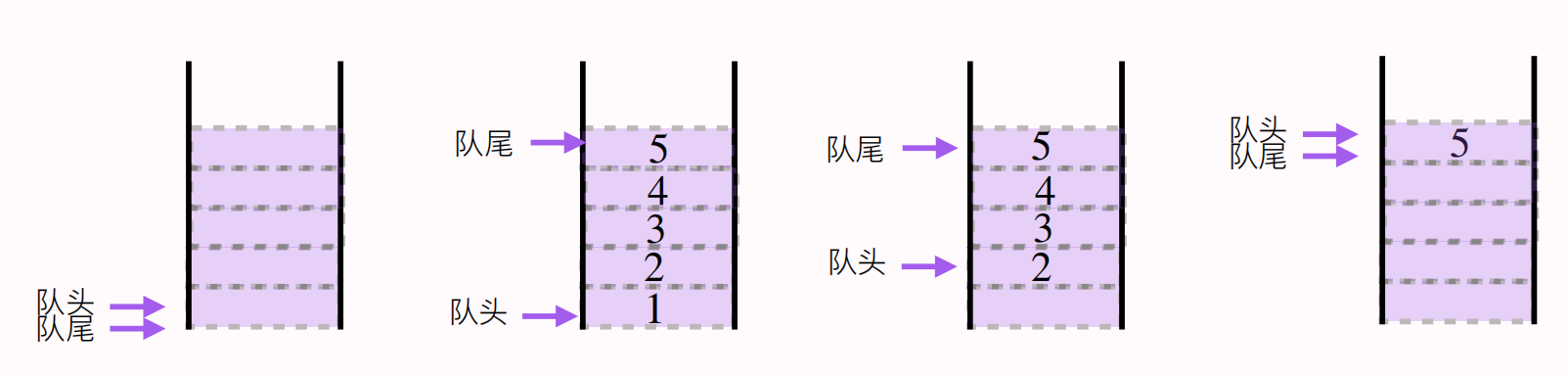
队列

和栈相反，是一种先进先出的线性表，它只允许在表的一端进行插⼊，而在另一端删除元素。

队尾：允许插⼊的一端

队头：允许删除的一端

队列的类型定义

ADT Queue {
    数据对象:
        D = {ai | aiElemSet, i=1,2...,n, n≥0}
    数据关系:
        R1 = {<ai-1, ai> | ai-1, ai ED, i=2,...,n}
        约定其中a1端为队列头， an端为队列尾
    基本操作:
        ...
} ADT Queue

队列的八大基本操作

1.InitQueue(&Q)

操作结果：构造一个空队列Q。

2.DestroyQueue(&Q)

初始条件：队列Q已存在。

操作结果：队列Q被销毁，不再存在。

3.QueueEmpty(Q)

初始条件：队列Q已存在。

操作结果：若Q为空队列，则返回TRUE，否则返回FALSE。

4.QueueLength(Q)

初始条件：队列Q已存在。

操作结果：返回Q的元素个数，即队列的长长度。

5.GetHead(Q, &e)

初始条件：Q为非空队列。

操作结果：用e返回Q的队头元素。

6.ClearQueue(&Q)

初始条件：队列Q已存在。

操作结果：将Q清为空队列。

7.EnQueue(&Q, e)

初始条件：队列Q已存在。

操作结果：插⼊入元素e为Q的新的队尾元素。

8.DeQueue(&Q, &e)

初始条件：Q为非空队列。

操作结果：删除Q的队头元素，并用用e返回其值。

⼩节2 队列类型的实现

链队列

用链表表示的队列称为链队列。一个链队列显然需要两个分别指示对头和对尾的指针才能唯一确定。

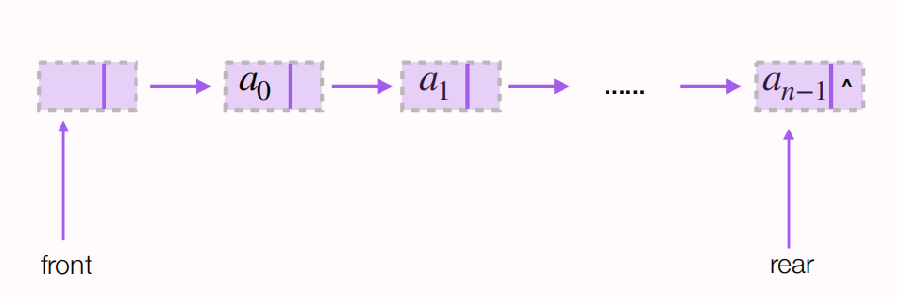
链队列的类型定义

typedef struct QNode {  // 结点类型
    QElemType       data;
    struct QNode    *next;
} QNode, *QueuePtr;

Status EnQueue(LinkQueue &Q, QElemType e)
{
    // 插入元素e为Q的新的队尾元素
    p = new QNode;
    if (!p) {
        // 存储分配失败
        exit(OVERFLOW);
    }
    p->data = e;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
    
    return OK;
}

Status DeQueue(LinkQueue &Q, QElemType &e) 
{
    if (Q.front == Q.raer) {
        return ERROR;
    }
    p = Q.front->next;
    e = p->data;
    Q.front->next = p->next;
    delete(p);
    
    return OK;
}

循环队列

在顺序队列中，当队尾指针已经到数组的上界，不能再有入队操作，但其实数组中还有空位置，这就叫做“假溢出”，解决假溢出的途径—-采用用循环队列。

队空条件：front ==rear

队满条件：front==（rear+1）%N

队列长度：L=（N+rear-front）%N

循环队列的类型定义

#define MAXQSIZE 100  // 最大队列长度

typedef struct {
    QElemType *base;  // 动态分配存储空间
    int front;  // 头指针，若队列不为空，指向队列头元素
    int rear;  // 尾指针，若队列不为空，指向队列尾元素的下一个位置
    int queuesize;
} SqQueue;

Status InitQueue(SqQueue &Q, int maxsize)
{
    Q.base = new ElemType[maxsize];
    if (!Q.base) {
        exit(OVERFLOW);
    }
    Q.queuesize = maxsize;
    Q.front = Q.rear = 0;
    
    return OK;
}

Status EnQueue(SqQueue &Q, ElemType e)
{
    // 插入元素e为Q的新的队尾元素
    if ((Q.rear + 1) % Q.queuesize == Q.front) {
        // 队列满
        return ERROR;
    }
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear + 1) % Q.queuesize;
    
    return OK;
}

Status DeQueue(SqQueue &Q, ElemType &e)
{
    if (Q.front == Q.rear) {
        return ERROR;
    }
    e = Q.base[Q.front];
    Q.front = (Q.front + 1) % Q.queuesize;
    
    return OK;
}

循环队列与循环链表的区别

队列（包括循环队列）是一个逻辑概念，而链表是一个存储概念。一个队列是否是循环队列，不取决于它将采用何种存储结构，根据实际的需要，循环队列可以采用顺序存储结构，也可以采用链式存储结构，包括采用循环链表作为存储结构。

例题3-3

栈和队列的相同之处是

A．元素的进出满⾜先进后出 B．元素的进出满⾜先进先出 C．只允许在端点进行插入和删除操作 D．无无共同点

例题3-4 Q是一个队列，S是一个空栈，实现将队列中的元素逆置的算法。
例题3-5 简述栈和线性表的差别

例题解析

解析3-1
解析3-2 B
解析3-3 C

本题考查堆栈和队列的特点。堆栈和队列是常用的两种数据结构，其中队列只允许在一端进行插入，另一端进行删除操作，具有先进先出的特征。而堆栈只允许在同一端进行插⼊和删除运算，具有后进先出的特征。因此，堆栈和队列的相同之处是允许在端点进行插⼊和删除操作。

解析3-4

算法思想：将队列中的元素逐个地出队列，入栈：全部⼊栈后再逐个出栈，入队列。

void inverse (Stack &S, Queue &Q)
{
    ElemType x;
    while (!QueueEmpty(Q)) {
        DeQueue(Q, x);  // 队列中全部元素依次出队
        Push(S, x);  // 元素依次入栈
    }
    while(!StackEmpty(S)) {
        pop(S, x);  // 栈中全部元素依次出栈
        EnQueue(Q, x);  // 再入队        
    }
}

解析3-5

线性表是具有相同特性的数据元素的一个有限序列。栈是限定仅在表尾进行插入和删除操作的线性表。

正文

模块1 栈

⼩节1 栈的类型定义

⼩节2 栈的应用举例

⼩节3 栈类型的实现

模块2 队列

⼩节1 队列的类型定义

⼩节2 队列类型的实现

例题解析

参考资料